



Next: Szeregi Fouriera
Up: Zadania z matematyki dla
Previous: Funkcje zmiennej zespolonej
Contents
- Wykaż, że funkcja
 jest rozwiązaniem odpowiedniego
równania różniczkowego:
jest rozwiązaniem odpowiedniego
równania różniczkowego:
(a)
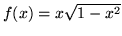
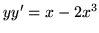
(b)
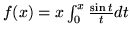
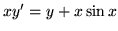
- Podaj całki ogólne i szczególne poniższych równań:
(a) 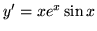
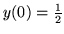 (b)
(b)
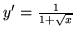
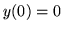
- Rozwiązaniem ogólnym pewnego równania różniczkowego jest
funkcja
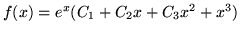 . Znajdż całkę
szczególną spełniającą warunki początkowe
. Znajdż całkę
szczególną spełniającą warunki początkowe
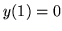 ,
, 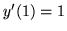 ,
, 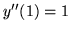 .
.
- Znajdź równanie różniczkowe rodziny krzywych (gdzie
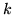 jest parametrem):
jest parametrem):
(a) 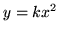 (b)
(b)
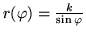
- Narysuj pole kierunków równania
(a) 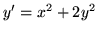 (b)
(b) 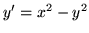 .
.
- Rozwiąż równania:
(a)
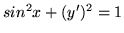 (b)
(b)
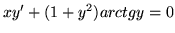
(c) 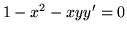
- Znajdź całki szczególne równań:
(a)
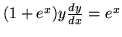 ,
, 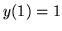
(b)
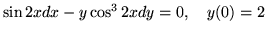
(c)
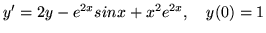
- Rozwiąż równania
(a) jednorodne: 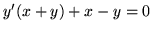 ,
,
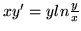 ,
,
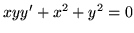
(b) sprowadzalne do jednorodnych:
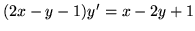 ,
,
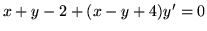 ,
,
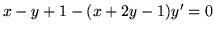 ,
,
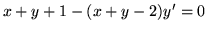
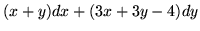 ,
, 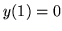
- Rozwiąż równania:
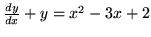 ,
, 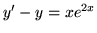 ,
,
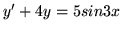
- Znajdż całki szczególne równań:
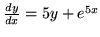
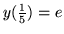
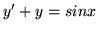
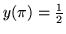
- Wyznacz czynnik całkujący i rozwiąż
równania różniczkowe wiedząc, że istnieje czynnik
całkujący zależny od jednej zmiennej.
- Wykaż, że dla równania
(gdzie 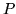 i
i 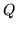 są funkcjami klasy
są funkcjami klasy 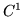 w
w
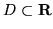 )
istnieje czynnik całkujący postaci
)
istnieje czynnik całkujący postaci 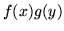 jeśli
istnieją funkcje
jeśli
istnieją funkcje 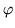 i
i 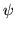 spełniające równanie
spełniające równanie
i wtedy
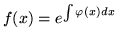 i
i
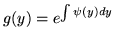 .
Korzystając z powyższego, znajdż czynnik całkujący
i rozwiąż równanie
.
Korzystając z powyższego, znajdż czynnik całkujący
i rozwiąż równanie
(a)
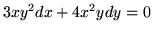
(b)
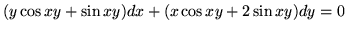
- Rozwiąż równania:
- Rozwiąż równania:
- Sprawdż, że jeśli
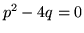 wtedy
wtedy 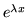 oraz
oraz
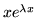 są dwoma
liniowo niezależnymi rozwiązaniami równania
są dwoma
liniowo niezależnymi rozwiązaniami równania
(gdzie 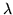 jest jedynym rozwiązaniem równania
charakterystycznego).
jest jedynym rozwiązaniem równania
charakterystycznego).
- Podaj rozwiązania ogólne równań różniczkowych:
- Dla równań z zadania poprzedniego znajdż rozwiązania
spełniające warunki początkowe
- Wykaż, że jeśli
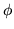 jest całką szczególną
równania
jest całką szczególną
równania
zaś 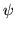 równania
równania
wówczas 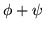 jest całką szczególną równania
jest całką szczególną równania
- Wykaż, że jeśli
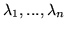 są
różnymi pierwiastkami równania
są
różnymi pierwiastkami równania
wtedy funkcje
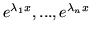 tworzą układ podstawowy tego równania.
tworzą układ podstawowy tego równania.
- Rowiąż (jeśli się da, to zarówno metodą
wariacji stałych jak i metodą przewidywania)
równania:
- Rozwiąż w przedziale
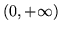 równanie
równanie
wiedząc, że 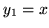 oraz
oraz 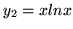 tworzą układ fundamentalny
rozwiązań równania
tworzą układ fundamentalny
rozwiązań równania
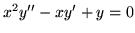
- Rozwiąż:
- Sprowadż poniższe układy równań liniowych do
równań liniowych odpowiedniego rzędu:
- Niech
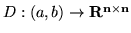 ,
,
Wykaż, że jeżeli
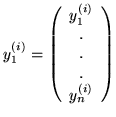
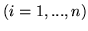 , są rozwiązaniami układu
równań liniowych jednorodnych:
, są rozwiązaniami układu
równań liniowych jednorodnych:
i
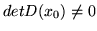 dla pewnego
dla pewnego 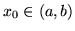 , wtedy
, wtedy 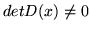 dla każdego
dla każdego 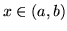 .
.
- Sprawdź, że funkcje
(a)
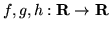 (b)
(b)
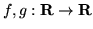
są liniowo niezależnymi rozwiązaniami ukladu 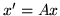 , gdzie
, gdzie
(a)
![$ A=\left[
\begin{array}{ccc}
2 & 0 & 1\\
1 & 1 & 0\\
0 & 0 & 0
\end{array}
\right]
$](img799.gif) (b)
(b)
![$A = \left[
\begin{array}{cc}
1 & 0\\
1 & 1
\end{array} \right]
$](img800.gif)
- Rozwiąż układy równań:
(a) 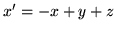 ,
, 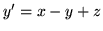 ,
, 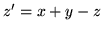
(b)
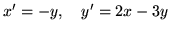
(c)
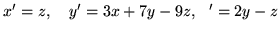
(d)
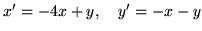
(e)
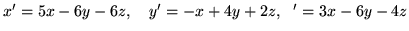
(f)
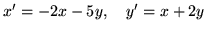
(g)
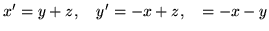
(h)
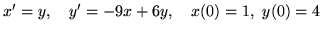
(i)
![$x'=\left[ \begin{array}{cc}
1 & 0\\
1 & 1
\end{array} \right] x
+ \left[ \begin{array}{c} 2 \\ 3 \end{array}
\right] $](img811.gif)
(j)
![$x'=\left[ \begin{array}{ccc}
-9 & 2 & 6\\
5 & 0 & -3\\
-16 & 4 & 11
\end{array} \right] x
+ \left[ \begin{array}{c} 2 \\ 2 \\ 3 \end{array}
\right] $](img812.gif)
(k)
![$x'=\left[ \begin{array}{cc}
0 & 1\\
2 & 1
\end{array} \right] x
+ \left[ \...
...ay}
\right] , \ \ \ x(0)=\left[ \begin{array}{c} -1\\ 1,7 \end{array} \right] $](img813.gif)
(l)
![$x'=\left[ \begin{array}{cc}
-2 & -5\\
1 & 0
\end{array} \right] x
+ \left[ \begin{array}{c} 3 \\ -2 \end{array} \right] $](img814.gif)
(m) 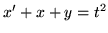 ,
, 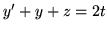 ,
, 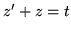
(n) 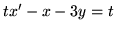
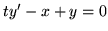
(o) 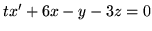
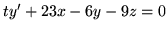
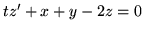
(p) 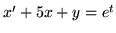




Next: Szeregi Fouriera
Up: Zadania z matematyki dla
Previous: Funkcje zmiennej zespolonej
Contents
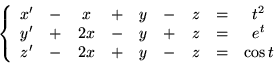
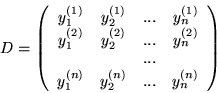

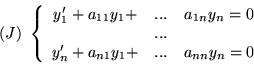
![$ A=\left[
\begin{array}{ccc}
2 & 0 & 1\\
1 & 1 & 0\\
0 & 0 & 0
\end{array}
\right]
$](img799.gif) (b)
(b)
![$A = \left[
\begin{array}{cc}
1 & 0\\
1 & 1
\end{array} \right]
$](img800.gif)
![$x'=\left[ \begin{array}{cc}
1 & 0\\
1 & 1
\end{array} \right] x
+ \left[ \begin{array}{c} 2 \\ 3 \end{array}
\right] $](img811.gif)
![$x'=\left[ \begin{array}{ccc}
-9 & 2 & 6\\
5 & 0 & -3\\
-16 & 4 & 11
\end{array} \right] x
+ \left[ \begin{array}{c} 2 \\ 2 \\ 3 \end{array}
\right] $](img812.gif)
![$x'=\left[ \begin{array}{cc}
0 & 1\\
2 & 1
\end{array} \right] x
+ \left[ \...
...ay}
\right] , \ \ \ x(0)=\left[ \begin{array}{c} -1\\ 1,7 \end{array} \right] $](img813.gif)
![$x'=\left[ \begin{array}{cc}
-2 & -5\\
1 & 0
\end{array} \right] x
+ \left[ \begin{array}{c} 3 \\ -2 \end{array} \right] $](img814.gif)