![]() - zasada wyłączonego środka
- zasada wyłączonego środka
![]() - zasada transpozycji
- zasada transpozycji
![]() - zasada podwójnego
zaprzeczenia
- zasada podwójnego
zaprzeczenia
![]()
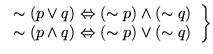 - prawa de Morgana
- prawa de Morgana
(a)
![]()
![]() (b)
(b)
![]()
- (a)
-
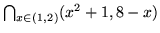
- (b)
-
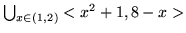
1.
![]()
![]()
2. ![]()
![]()
![]()
![]() .
.
Sformułuj odpowiednie warunki dla kresu dolnego.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(a) ![]() (b)
(b) ![]() .
.
Napisz równanie prostej praechodzącej przez
- -
- prostopadłej do
- -
- równoległej do
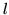 .
.
- -
- płaszczyzny
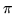 w której leżą
w której leżą 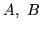 i
i 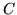 ,
,
- -
- prostej prostopadłej do
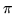 przechodzącej przez
przechodzącej przez 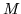 .
.
- -
- płaszczyzny
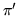 równoległej do
równoległej do 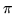 przechodzącej przez
przechodzącej przez 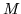 ,
,
- -
- sfery o środku w
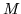 stycznej do
stycznej do 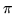 .
.
- -
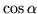 i
i 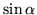 , gdzie
, gdzie 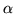 jest kątem pomiędzy
wektorami
jest kątem pomiędzy
wektorami 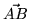 oraz
oraz 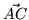 ,
,
- -
- objętość równoległościanu którego krawędziami są
odcinki
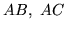 i
i 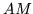 .
.
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(i)
(ii)
(i)
(ii)
(iii)
(b) Przedział
Udowodnij, że jeśli