



Next: Rachunek różniczkowy funkcji jednej
Up: Zadania z matematyki dla
Previous: Wiadomości wstępne
Contents
- Podaj definicje Heinego i Cauchy'ego granicy
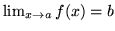 , gdzie
, gdzie
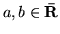 .
.
- Wykaż równoważność definicji Heinego i Cauchy'ego
granicy funkcji (także
w przypadku granic niewłaściwych).
- Znajdź granicę
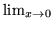
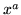 ,
, 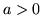 .
.
- Korzystając z definicji Heinego granicy funkcji wykaż, że
(a)
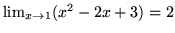
(b)
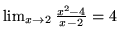
(c)
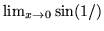 nie istnieje.
nie istnieje.
- Korzystając z definicji Cauchy'ego granicy, wykaż, że
.
- Oblicz granice:
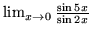 ,
,
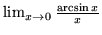 ,
,
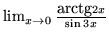 ,
,
- Udowodnij, że: (i)
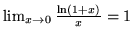 ,
(ii)
,
(ii)
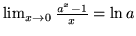 .
.
- Oblicz granice:
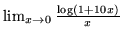 ,
,
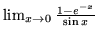 ,
,
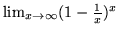 ,
,
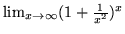 .
.
- Wykaż ciągłość funkcji
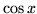 (w R) i
(w R) i 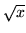 (w
(w 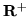 ).
).
- Dla jakiej wartości a funkcja
jest ciągła.
- Zdefiniuj wartości poniższych funkcji w 0 tak, by były
ciągłe w R:
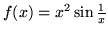 ,
,
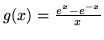 .
.
- Zbadaj ciągłość funkcji :
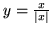 ,
,
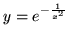 ,
,
- Zbadać ciągłość i narysuj wykresy funkcji :
(a)
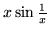 (b) sgnx.
(b) sgnx.
- Wykaż, że równanie
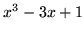 ma
pierwiastek rzeczywisty. Znajdź jego wartość przybliżoną.
ma
pierwiastek rzeczywisty. Znajdź jego wartość przybliżoną.
- Wykaż, że jeśli ciągi
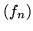 i
i 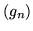 funkcji,
funkcji, 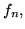 ,
,
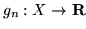 ,
,
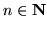 , są jednostajnie zbieżne do funkcji
, są jednostajnie zbieżne do funkcji  i
i 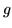 to
to
(A) ciąg 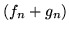 jest jednostajnie zbieżny do
jest jednostajnie zbieżny do 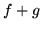
(B) ciąg 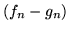 jest jednostajnie zbieżny do
jest jednostajnie zbieżny do 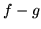
(C) ciąg
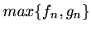 jest jednostajnie zbieżny do
jest jednostajnie zbieżny do
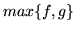
(D) ciąg
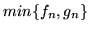 jest jednostajnie zbieżny do
jest jednostajnie zbieżny do
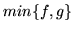 ,
,
gdzie
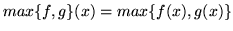 .
.
- Czy ciąg funkcyjny
(a)
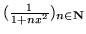 , dla
, dla 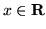 , (b)
, (b)
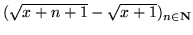 ,
dla
,
dla 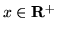 ,
,
(c) 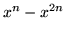 ,
, 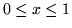 ,
(d)
,
(d) 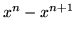 ,
, 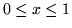 ,
,
(e)
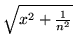 ,
,
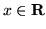 ,
(f)
,
(f)
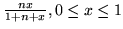 ,
,
(g)
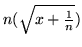 ,
, 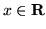 .
.
jest jednostajnie zbieżny ?
- Oblicz odległość Czebyszewa funkcji
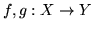 jeżeli
jeżeli 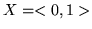 ,
, 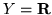 ,
, 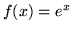 ,
,
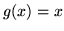 .
.




Next: Rachunek różniczkowy funkcji jednej
Up: Zadania z matematyki dla
Previous: Wiadomości wstępne
Contents