



Next: Rachunek całkowy zmiennej rzeczywistej
Up: Zadania z matematyki dla
Previous: Granice i ciągłość funkcji
Contents
- Wyjaśnij co oznacza:
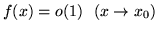 .
.
- Uzasadnij wzory:
-
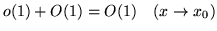
-
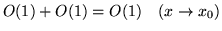
-
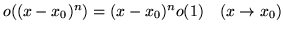
-
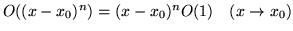
-
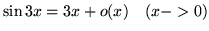
- Znajdź rzędy nieskonczenie małych:
-
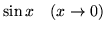
-
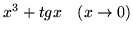
- Mówimy, że funkcje
 i
i 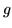 są równoważne dla
są równoważne dla
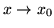 ,
jezeli istnieje
taka funkcja
,
jezeli istnieje
taka funkcja 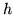 , że
, że 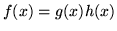 ,
,
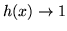 dla
dla
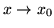 .
Piszemy wtedy
.
Piszemy wtedy 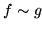 , (
, (
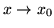 ).
).
Wykaż, że:
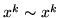 ,
,
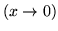
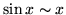 ,
,
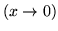
-
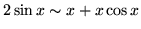 ,
,
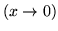
-
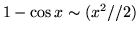 ,
,
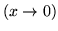
Mówimy, że 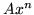 jest częścią główną funkcji
jest częścią główną funkcji  dla
dla
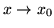 jeśli
jeśli
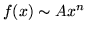 ,
,
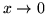 .
.
Określ 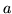 i
i
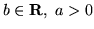 , tak by funkcja
, tak by funkcja
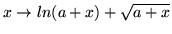 była nieskończenie małą możliwie najwyższego rzędu. Jaka jest wtedy
jej część głowna?
była nieskończenie małą możliwie najwyższego rzędu. Jaka jest wtedy
jej część głowna?
- Z definicji oblicz pochodne funkcji:
(a)
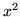 (b)
(b) 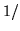 (c)
(c) ![$\sqrt[3]{x}$](img199.gif) (d)
(d) 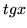 (e)
(e) 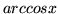
- Wykaż, że jeśli
 jest różniczkowalna w
jest różniczkowalna w 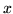 , to
, to
![\begin{displaymath}
\lim_{n\rightarrow +\infty}n[f(x+1/ń)-f(x)]=f'(x).
\end{displaymath}](img203.gif) |
(5.1) |
Posłuż się funkcją Dirichleta
do wykazania, że spełnienie warunku (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) nie jest wystarczające do
istnienia pochodnej w punkcie x .
) nie jest wystarczające do
istnienia pochodnej w punkcie x .
- Użyj różniczki do obliczenia wartości przybliżonych następujących
wyrażeń:
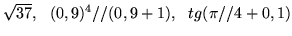 .
.
- Niech
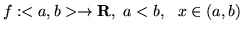 .
Jeżeli istnieje granica
.
Jeżeli istnieje granica
wtedy nazywamy ją pochodną prawostronną funkcji  w punkcie
w punkcie 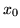 ,
jeżeli istnieje granica
,
jeżeli istnieje granica
wtedy nazywamy pochodną lewostronną funkcji f w punkcie 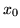 , a jeśli
istnieje
, a jeśli
istnieje
nazywamy ją wtedy pochodną symetryczną funkcji  w punkcie
w punkcie 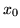 .
.
a) Udowodnij, że funkcja różniczkowalna w punkcie 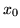 , ma w
, ma w 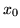 pochodne prawo- i lewostronną.
pochodne prawo- i lewostronną.
b) Wykaż, że jeśli  ma w
ma w 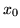 pochodną lewostronną i
prawostronną,
wtedy
pochodną lewostronną i
prawostronną,
wtedy  ma w
ma w 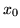 pochodną symetryczn.
pochodną symetryczn.
c) Niech
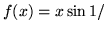 dla
dla 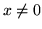 i
i 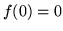 .
Udowodnij, że
.
Udowodnij, że  ma w
ma w 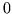 pochodną symetryczną, lecz nie ma ani
pochodnej prawostronnej, ani pochodnej lewostronnej w tym punkcie.
pochodną symetryczną, lecz nie ma ani
pochodnej prawostronnej, ani pochodnej lewostronnej w tym punkcie.
- Niech
Tak dobierz 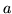 i
i 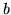 , żeby funkcja
, żeby funkcja
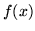 była różniczkowalna w
była różniczkowalna w 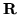 .
.
- Znajdź pochodne funkcji zdefiniowanych wzorami:
-
![$f(x)=\frac{x}{(1-x)^2(1+x^3)} \ \ f(x)=\sqrt{x+\sqrt{x+\sqrt{x}}} \ \
f(x)=\sqrt[3]{\frac{1+x^3}{1-x^3}}$](img218.gif)
-
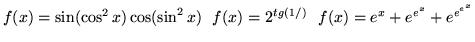
-
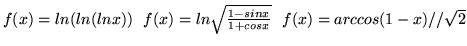
-
![$f(x)=ln(1+\sin^2x)-(\sin x)(arctg(\sin x)) \ \
f(x)=arctg(x+\sqrt{1+x^2})
\ \ f(x)=\sqrt[x]{x}$](img221.gif)
-
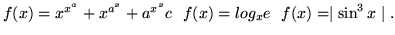
W każdym z przykładów  jest funkcja rzeczywistą o wartościach
rzeczywistych i dziedzinie naturalnej.
jest funkcja rzeczywistą o wartościach
rzeczywistych i dziedzinie naturalnej.
- Niech
Wykaż, że  spełnia w
spełnia w 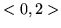 założenia twierdzenia
Lagrange'a i wskaż
założenia twierdzenia
Lagrange'a i wskaż 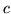 ,
dla którego
,
dla którego
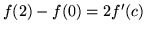 .
.
- Wykaż nierówności:
- (a)
-
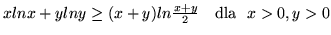
- (b)
-
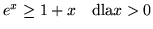
- (c)
-
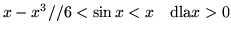 .
.
- Oblicz następujące granice:
-
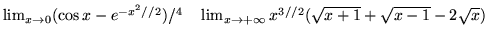
-
![$\lim_{x\rightarrow +\infty}(\sqrt[6]{x^6+x^5} - \sqrt[6]{x^6-x^5}) \ \ \
\lim_{x\rightarrow 0}(1-(\cos x)^{\sin x})/ź^3 $](img231.gif)
-
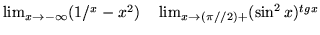
- Dla jakich wartości
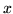 wielomian
wielomian 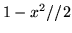 przybliża funkcję
przybliża funkcję 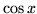 z dokładnością do co najmniej
z dokładnością do co najmniej 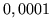 .
.
- Oblicz z pomocą wzoru Taylora, następujące wielkości:
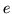 z dokładnością do
z dokładnością do 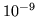
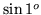 ż dokładnością do
ż dokładnością do 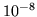
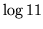 z dokładnością do
z dokładnością do 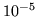
- Zbadaj wykresy funkcji:
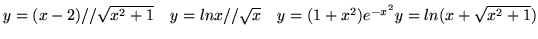 .
.




Next: Rachunek całkowy zmiennej rzeczywistej
Up: Zadania z matematyki dla
Previous: Granice i ciągłość funkcji
Contents
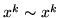 ,
,
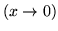
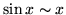 ,
,
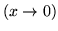
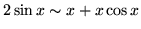 ,
,
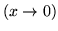
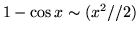 ,
,
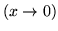
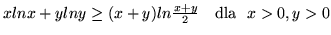
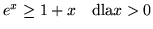
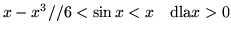 .
.
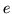 z dokładnością do
z dokładnością do 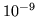
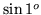 ż dokładnością do
ż dokładnością do 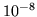
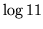 z dokładnością do
z dokładnością do 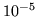
![$f(x)=\frac{x}{(1-x)^2(1+x^3)} \ \ f(x)=\sqrt{x+\sqrt{x+\sqrt{x}}} \ \
f(x)=\sqrt[3]{\frac{1+x^3}{1-x^3}}$](img218.gif)