



Next: Przestrzenie refleksywne
Up: Programowanie matematyczne i układy
Previous: Zbiory i funkcjonały wypukłe
Spis rzeczy
Niech zbiór
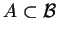 jest zwarty. Wtedy
zachodzi następujące twierdzenie
jest zwarty. Wtedy
zachodzi następujące twierdzenie
2.1
Twierdzenie Niech funkcjonał
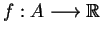
jest tylko ciągły. Wtedy istnieje taki element
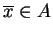
, że zachodzi równość:
![$\displaystyle f[\overline{x}]=\min_{x\in\, A}f[x]$](img20.gif) |
(2.1) |
tj.
![$ f[\overline{x}]\leq f[x]$](img21.gif)
dla wszystkich
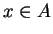
Dowód jest prosty, oparty na pojęciu zwartości zbioru
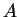 .
.
Niestety warunek ciągłości jest bardzo silnym, tj.
ograniczającym klasę funkcjonałów.
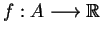 .
.
Okazuje się, że wystarczy założyć, że funkcjonał
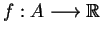 jest semi-ciągłym z dołu na
jest semi-ciągłym z dołu na 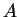 , tj. dla
każdego
, tj. dla
każdego 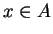 oraz ciągu
oraz ciągu
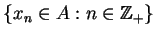 takiego, że
takiego, że
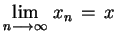 |
(2.2) |
zachodzi nierówność
W przypadku Tw.2 zbiór zwarty
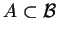 okazuje
się bardzo małym, nie zawierającym punktów wewnętrznych,
ponieważ prawdziwe jest takie twierdzenie o zbiorach w
okazuje
się bardzo małym, nie zawierającym punktów wewnętrznych,
ponieważ prawdziwe jest takie twierdzenie o zbiorach w
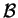 .
.
2.2
Twierdzenie Zbiór
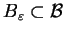
, gdzie
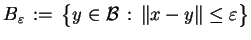 |
(2.3) |
jest zwarty w
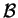 wtedy i tylko wtedy
wtedy i tylko wtedy
gdy
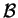
jest skończeniewymiarowy, tj.
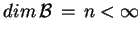
.
2.3
Definicja Niech
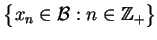
będzie ciągiem elementów przestrzeni
Banacha
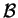
, i niech
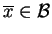
. Mówimy, że
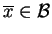
jest
stałą granicą ciągu
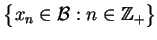
(i piszemy
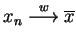
), jeśli
dla dowolnego liniowego, ciągłego funkcjonału
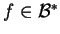
zachodzi równość
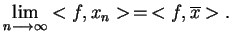 |
(2.4) |
Definicja ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ma sens ponieważ gdy
ma sens ponieważ gdy
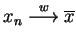 oraz
oraz
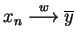 ,
,
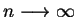 , to można łatwo wykazać, że
, to można łatwo wykazać, że
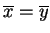 , tj. granica
, tj. granica
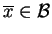 jest jedyna.
jest jedyna.
2.4
Definicja Mówimy, że zbiór
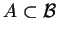
przestrzeni Banacha
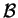
jest
słabo zwartym, jeżeli z dowolnego ciągu
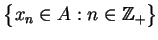
można wybrać
podciąg słabo zbieżny do pewnego elementu
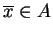
, tj.
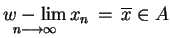
(albo
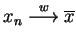
).
2.5
Definicja Niech
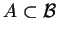
oraz
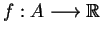
będzie określonym na
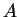
funkcjonałem. Mówimy, że funkcjonał
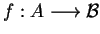
jest
słabo semi-ciągłym z dołu na
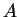
,
jeśli
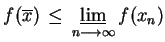 |
(2.5) |
dla każdego słabo zbieżnego do
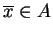
ciągu
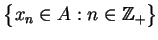
, tj.
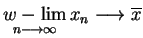
.
Następne twierdzenie jest ważne dla wielu zagadnień w
przestrzeni Banacha
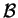 .
.
2.6
Twierdzenie Niech
i)
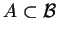
jest niepustym, słabo zwartym zbiorem
przestrzeni Banacha
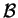
;
ii)
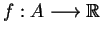
jest słabo semi-ciągłym
funkcjonałem
Wtedy:
a)
![$ \underset{x\in\, A}{\inf}\,f[x]>-\infty$](img43.gif)
b) istnieje przynajmniej jeden element
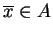
, taki
że
![$\displaystyle f[\overline{x}]\,=\,\inf_{x\in\, A}\,f[x]$](img44.gif) |
(2.6) |
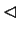 Pokażemy dowód b), skąd będzie wynikało a).
Pokażemy dowód b), skąd będzie wynikało a).
Niech
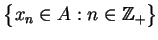 będzie
ciągiem elementów z
będzie
ciągiem elementów z 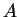 minimalizującym
minimalizującym
![$ \underset{x\in\, A}{\inf}\,f[x]$](img45.gif) , tj.
, tj.
![$\displaystyle \lim_{n\longrightarrow \infty}\,f[x_{n}]\,=\,\inf_{x\in\,
A}\,f[x],$](img46.gif) |
(2.7) |
która zawsze istnieje na mocy definicji operacji inf.
Ponieważ zbiór 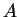 jest słabo zwarty, istnieje podzbiór
jest słabo zwarty, istnieje podzbiór
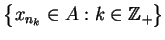 oraz
element
oraz
element
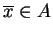 , takie, że
, takie, że
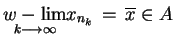 . Dalej z tego, że funkcjonał
. Dalej z tego, że funkcjonał
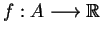 jest słabo semi-ciągłym z dołu na
jest słabo semi-ciągłym z dołu na 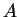 ,
otrzymujemy że
,
otrzymujemy że
![$\displaystyle f[\overline{x}]\,\leq\,\underset{n\longrightarrow\infty}{\underli...
...\,\equiv\,
\lim_{n\longrightarrow\infty}\,f[x_{n}]\,=\,\inf_{x\in\,
A}\,f[x].$](img49.gif) |
(2.8) |
Z drugej strony z (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) otrzymujemy, że
) otrzymujemy, że
![$\displaystyle f[\overline{x}]\,\geq\,\inf_{x\in \,A}\,f[x].$](img50.gif) |
(2.9) |
Teraz z (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) oraz (
) oraz (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) dostajemy:
) dostajemy:
![$\displaystyle f[\overline{x}]\,=\,\inf_{x\in\, A}f[x],$](img51.gif) |
(2.10) |
gdzie
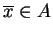 . Z tego teraz, że
. Z tego teraz, że
![$ f[\overline{x}]\neq -\infty$](img52.gif) , otrzymujemy, że
, otrzymujemy, że
![$ f[x]>-\infty$](img53.gif) dla wszystkich
dla wszystkich 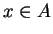 , co jest
równoważne
, co jest
równoważne
![$ \underset{x\in\, A}{\inf}\,f[x]>-\infty$](img43.gif)




Next: Przestrzenie refleksywne
Up: Programowanie matematyczne i układy
Previous: Zbiory i funkcjonały wypukłe
Spis rzeczy
![]() .
.
![]() jest semi-ciągłym z dołu na
jest semi-ciągłym z dołu na ![]() , tj. dla
każdego
, tj. dla
każdego ![]() oraz ciągu
oraz ciągu
![]() takiego, że
takiego, że
![]() okazuje
się bardzo małym, nie zawierającym punktów wewnętrznych,
ponieważ prawdziwe jest takie twierdzenie o zbiorach w
okazuje
się bardzo małym, nie zawierającym punktów wewnętrznych,
ponieważ prawdziwe jest takie twierdzenie o zbiorach w
![]() .
.
![]() ma sens ponieważ gdy
ma sens ponieważ gdy
![]() oraz
oraz
![]() ,
,
![]() , to można łatwo wykazać, że
, to można łatwo wykazać, że
![]() , tj. granica
, tj. granica
![]() jest jedyna.
jest jedyna.
![]() .
.
![]() będzie
ciągiem elementów z
będzie
ciągiem elementów z ![]() minimalizującym
minimalizującym
![]() , tj.
, tj.