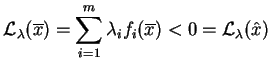Next: Dualność problemów programownia liniowego.
Up: Programowanie matematyczne i układy
Previous: Programowanie wypukłe. Wstęp.
Spis rzeczy
Niech
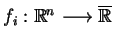 ,
,
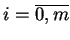 , będą funkcjami
, będą funkcjami
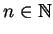 zmiennych. Zachodzi następujące
twierdzenie:
zmiennych. Zachodzi następujące
twierdzenie:
8.1
Twierdzenie (Lagrange'a). Niech
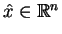
będzie ekstremum lokalnym dla
problemu
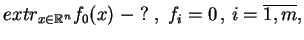 |
(8.1) |
a funkcje

,
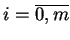
, są ciągle
różniczkowalne w otoczeniu punktu
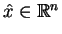
. Wtedy istnieje niezerowy wektor
mnożników Lagrange'a
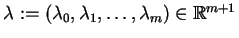
, taki, że dla funkcji
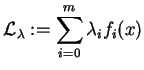 |
(8.2) |
spełniony jest
warunek stacjonarności:
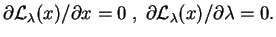 |
(8.3) |
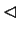 Dowód (niewprost). Przypuśćmy, że
warunek stacjonarności nie jest spełniony, tzn. że wektory
Dowód (niewprost). Przypuśćmy, że
warunek stacjonarności nie jest spełniony, tzn. że wektory
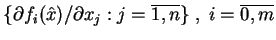 |
(8.4) |
są liniowo niezależne. To znaczy, że rząd macierzy
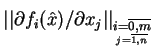 wynosi
wynosi
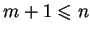 . Wtedy na mocy twierdzenia o rzędzie
istnieje macierz
. Wtedy na mocy twierdzenia o rzędzie
istnieje macierz
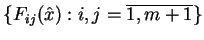 z wyznacznikiem różnym od zera. Przypuśćmy, że tą macierzą
jest macierz
z wyznacznikiem różnym od zera. Przypuśćmy, że tą macierzą
jest macierz
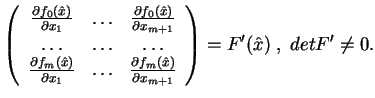 |
(8.5) |
Będziemy rozważać przypadek, kiedy
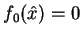 .
Jeśli tak nie jest, to funkcja
.
Jeśli tak nie jest, to funkcja
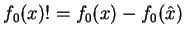 już spełnia ten
warunek.
już spełnia ten
warunek.
Weźmy wektor
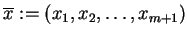 i zdefiniujmy odwzorowanie:
i zdefiniujmy odwzorowanie:
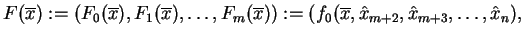 |
|
|
|
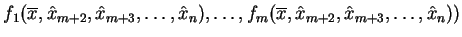 |
|
|
(8.6) |
Odwzorowanie
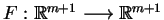 jest,
oczywiście, niezdegenerowane, ponieważ
jest,
oczywiście, niezdegenerowane, ponieważ
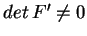 w
otoczeniu punktu
w
otoczeniu punktu
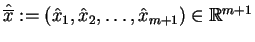 . Na mocy o
odwzorowaniu odwrotnym w
. Na mocy o
odwzorowaniu odwrotnym w
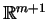 istnieje
odwrotne odwzorowanie
istnieje
odwrotne odwzorowanie
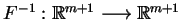 w otoczeniu punktu zero, takie,
że
w otoczeniu punktu zero, takie,
że
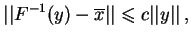 |
(8.7) |
gdzie 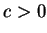 jest pewną stała. W szczególności dla
wystarczająco małego
jest pewną stała. W szczególności dla
wystarczająco małego
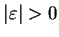 istnieje wektor
istnieje wektor
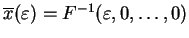 ,
taki, że
,
taki, że
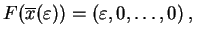 |
|
|
(8.8) |
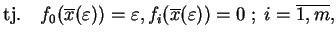 |
|
|
|
oraz spełnione są nierówności:
 |
(8.9) |
gdzie
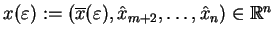 .
.
Tak więc z (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) i (
) i (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) otrzymujemy, że wektor
) otrzymujemy, że wektor
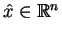 nie spełnia warunku ekstremalności, ponieważ w jego pobliżu isnieją wektory
nie spełnia warunku ekstremalności, ponieważ w jego pobliżu isnieją wektory
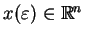 , na których funkcjonał
, na których funkcjonał
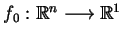 przyjmuje wartości zarówno większe, jak i mniejsze od
przyjmuje wartości zarówno większe, jak i mniejsze od
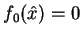 . A to przeczy temu, że
. A to przeczy temu, że
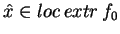 i kończy dowód.
i kończy dowód.

8.2
Uwaga. Warunek (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
) powoduje, oczywiście, że
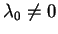
(
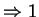
!), gdy wektory
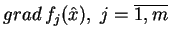
, są liniowo
niezależne.
Sformułujemy teraz warunki konieczne na ekstremum dla problemu z
równościa-mi i nierównościami w
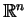 :
:
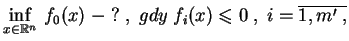 |
|
|
(8.10) |
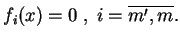 |
|
|
|
8.3
Twierdzenie. Niech
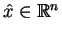
będzie minimum dla problemu (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
) i funkcji
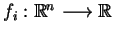
,
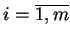
ciągłych i różniczkowalnych w
otoczeniu punktu
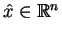
. Wtedy istnieje
niezerowy wektor mnożników Lagrange'a
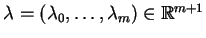
, taki, że dla funkcji Lagrange'a problemu
(
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
)
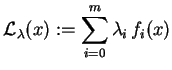 |
(8.11) |
w punkcie
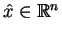
są spełnione
warunki:
- a)
- stacjonarności:
 |
(8.12) |
- b)
- dopełniającej elastyczności:
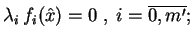 |
(8.13) |
- c)
- nieujemności:
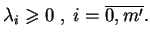 |
(8.14) |
 Dowód: Załóżmy, jak
wcześniej, że
Dowód: Załóżmy, jak
wcześniej, że
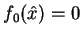 . Jeżeli
. Jeżeli
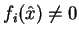 , i=
, i=
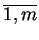 , to te
ograniczenia odrzucamy, ponieważ dla ekstremum lokalnego
ograniczenia
, to te
ograniczenia odrzucamy, ponieważ dla ekstremum lokalnego
ograniczenia
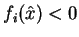 nie są ważne. Tym samym
można stwierdzić, że warunek dopełniającej elastyczności
jest spełniony.
nie są ważne. Tym samym
można stwierdzić, że warunek dopełniającej elastyczności
jest spełniony.
Niech teraz
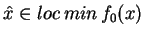 i
i
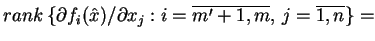
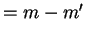 .
Wtedy dla
.
Wtedy dla
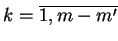 zbiory
zbiory
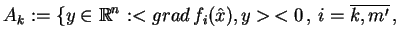 |
|
|
|
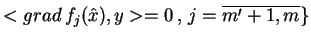 |
|
|
(8.15) |
dla
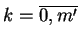 spełniają relacje:
spełniają relacje:
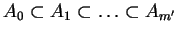 |
(8.16) |
oraz
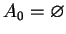 . Rzeczywiście, gdyby
. Rzeczywiście, gdyby
 , to istniałby wektor
, to istniałby wektor
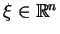 , taki, że
, taki, że
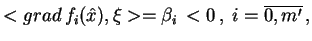 |
(8.17) |
gdzie
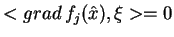 dla
dla
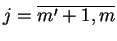 . Ponieważ odwzorowanie
. Ponieważ odwzorowanie
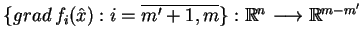 jest epimorfizmem, to dla dowolnych
jest epimorfizmem, to dla dowolnych
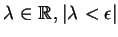 istnieje
odwzorowanie
istnieje
odwzorowanie
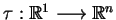 , takie, że
, takie, że
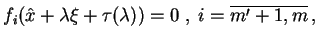 |
(8.18) |
gdzie
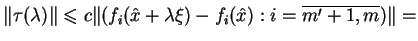 |
|
|
|
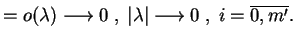 |
|
|
(8.19) |
Na mocy (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) otrzymujemy, że
) otrzymujemy, że
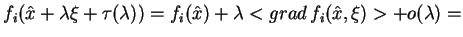 |
|
|
|
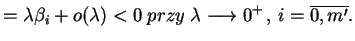 |
|
|
(8.20) |
Nierówność (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) znaczy, że przy
) znaczy, że przy
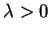 , wystarczająco mały element
, wystarczająco mały element
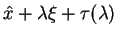 jest dopuszczalny dla
problemu (
jest dopuszczalny dla
problemu (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ), co przeczy temu, że
), co przeczy temu, że
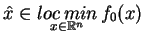 .
.
Dalej jest prawie oczywistym, że warunek stacjonarności funkcji Lagrange'a jest
spełniony przy warunku
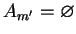 . W przeciwnym
przypadku
. W przeciwnym
przypadku
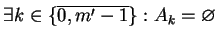 i
i
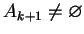 . Wtedy tylko
. Wtedy tylko
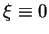 jest
rozwiązaniem problemu
jest
rozwiązaniem problemu
Rzeczywiście, niech
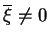 rozwiązuje
(
rozwiązuje
(![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ). Wtedy
). Wtedy
Niech teraz element
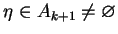 , tj.
, tj.
Wtedy dla
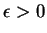 wystarczająco małego element
wystarczająco małego element
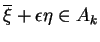 , co przeczy
założeniu, że
, co przeczy
założeniu, że
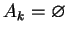 .
.
Dla zakończenia dowodu zastosujmy do problemu (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) twierdzenie Kuhna-Tuckera z warunkiem Slatera, ponieważ
) twierdzenie Kuhna-Tuckera z warunkiem Slatera, ponieważ
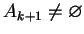 . Na mocy tego twierdzenia można
znaleźć takie nieujemne liczby
. Na mocy tego twierdzenia można
znaleźć takie nieujemne liczby
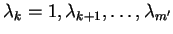 , że dla
funkcji Lagrange'a problemu (
, że dla
funkcji Lagrange'a problemu (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) )
)
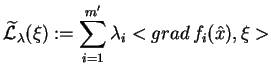 |
(8.23) |
w punkcie
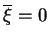 spełniony jest warunek
minimum, tj.
spełniony jest warunek
minimum, tj.
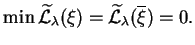 |
(8.24) |
Ostatnia równość (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) daje dla wszystkich
) daje dla wszystkich
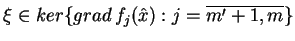
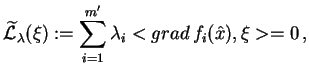 |
|
|
|
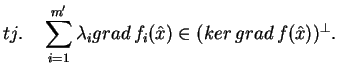 |
|
|
(8.25) |
To znaczy, że istnieją liczby
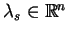 ,
,
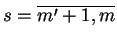 ,
takie, że
,
takie, że
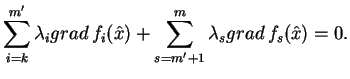 |
(8.26) |
Ale równość (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) jest dokładnie warunkiem
stacjonarności funkcji Lagrange'a
) jest dokładnie warunkiem
stacjonarności funkcji Lagrange'a
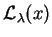 ,
,
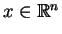 ,
,
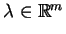 , przy założeniu
, przy założeniu
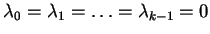 , co
kończy dowód.
, co
kończy dowód. 
8.4
Uwaga. Z twierdzenia
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
wnioskujemy, że przy
spełnieniu warunku
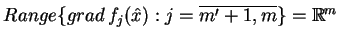
(tj. odwzorowanie
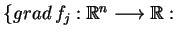
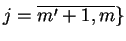
jest regularne w punkcie
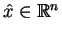
) oraz
istnieje element
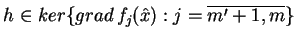
, dla którego
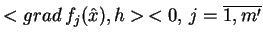
(analogia warunku Slatera!), wtedy
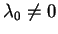
, i
można wziąć
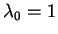
.
Twierdzenie ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) było bazowane na twierdzeniu
Kuhna-Tuckera, które formułuje-my i dowodzimy poniżej.
było bazowane na twierdzeniu
Kuhna-Tuckera, które formułuje-my i dowodzimy poniżej.
8.5
Problem programowania wypukłego:
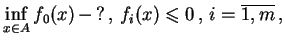 |
(8.27) |
gdzie
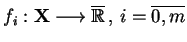
,
są wypukłe na
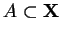
.
8.6
Lemat. Niech
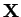
będzie przestrzenią
unormowaną. Wtedy minimum lokalne problemu (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
) jest
minimum globalnym.
8.7
Twierdzenie (Kuhna-Tuckera). Niech
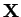
będzie
przestrzenią liniową,
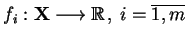
,
będą funkcjami wypukłymi na
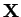
, a
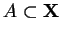
- podzbiorem wypukłym. Wtedy:
- i)
- Jeśli
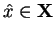 jest rozwiązaniem problemu programowania wypukłego,
to można znaleźć niezerowy wektor mnożników Lagrange'a
jest rozwiązaniem problemu programowania wypukłego,
to można znaleźć niezerowy wektor mnożników Lagrange'a
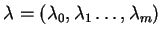 ,
taki, że dla funkcji Lagrange'a )
,
taki, że dla funkcji Lagrange'a )
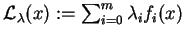 zachodzą:
zachodzą:
- a)
- zasada minimum dla
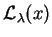
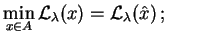 |
(8.28) |
- b)
- wrunek dopełniającej elastyczności
- c)
- warunek nieujemności :
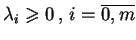 .
.
- ii)
- Jeśli
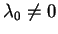 , to warunki a)-c) są wystrczające, żeby
, to warunki a)-c) są wystrczające, żeby
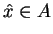 było rozwiązaniem.
było rozwiązaniem.
- iii)
- Dla tego, żeby
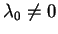 wystarczy wypełnienie warunku Statera, tj.
istnienia takiego punktu
wystarczy wypełnienie warunku Statera, tj.
istnienia takiego punktu
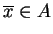 , dla którego
, dla którego
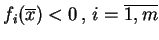 .
.
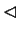 Niech
Niech
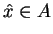 jest rozwiązaniem
(
jest rozwiązaniem
(![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ). Załóżmy także, że
). Załóżmy także, że
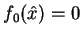 . Zdefiniujmy
. Zdefiniujmy
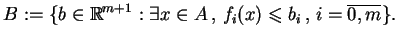 |
(8.29) |
a) Zbiór 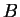 jest oczywiście niepusty i wypukły. Oprócz tego
jest oczywiście niepusty i wypukły. Oprócz tego
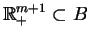 (przy
(przy
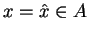 )! Zdefiniujmy zbiór
)! Zdefiniujmy zbiór
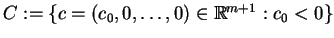 .
.
b) Zbiór  też jest niepusty i wypukły oraz
też jest niepusty i wypukły oraz
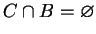 , ponieważ
, ponieważ
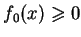 ,
,
 . Na mocy
twierdzenia o oddzielaniu zbiorów wypukłych istnieje wektor
. Na mocy
twierdzenia o oddzielaniu zbiorów wypukłych istnieje wektor
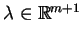 , taki, że
, taki, że
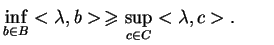 |
(8.30) |
Ponieważ 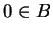 , to
, to
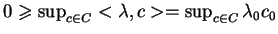 . Stąd mamy
. Stąd mamy
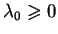
i
 . Nirówność (
. Nirówność (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) może być
teraz przepisana jako
) może być
teraz przepisana jako
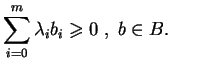 |
(8.31) |
c) Ponieważ
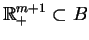 , z
(
, z
(![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) natychmiast
otrzymujemy, że
) natychmiast
otrzymujemy, że
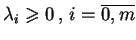 .
.
d) Sprawdzimy teraz, że zachodzi warunek dopełniającej
elastyczności
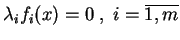 .
.
Weźmy  ; wtedy
; wtedy
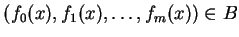 . Podstawiając
ten wektor do (
. Podstawiając
ten wektor do (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) otrzymamy
Ponieważ
) otrzymamy
Ponieważ
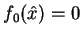 , z warunku
, z warunku
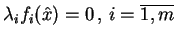 , dla
, dla
 mamy:
co udawadnia i).
mamy:
co udawadnia i).
e) Żeby udowodnić ii), połóżmy
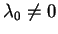 , tj.
, tj.
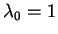 . Wtedy dla dowolnego dopuszczalnego
. Wtedy dla dowolnego dopuszczalnego
 otrzymujemy przy
otrzymujemy przy
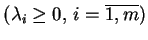
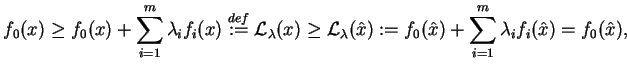 |
(8.32) |
tj.
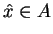 jest rozwiązaniem (
jest rozwiązaniem (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ).
).
Dla dowodu 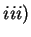 załóżmy, że zachodzi warunek Statera, oraz
załóżmy, że zachodzi warunek Statera, oraz
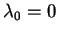 . Wtedy otrzymujemy, że dla
. Wtedy otrzymujemy, że dla
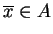
co jest sprzeczne z warunkiem
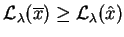 , co kończy dowód
, co kończy dowód 




Next: Dualność problemów programownia liniowego.
Up: Programowanie matematyczne i układy
Previous: Programowanie wypukłe. Wstęp.
Spis rzeczy
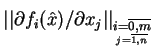 wynosi
wynosi
![]() i
i
![]()
![]() .
Wtedy dla
.
Wtedy dla
![]() zbiory
zbiory
![]() . W przeciwnym
przypadku
. W przeciwnym
przypadku
![]() i
i
![]() . Wtedy tylko
. Wtedy tylko
![]() jest
rozwiązaniem problemu
jest
rozwiązaniem problemu
![]() ) twierdzenie Kuhna-Tuckera z warunkiem Slatera, ponieważ
) twierdzenie Kuhna-Tuckera z warunkiem Slatera, ponieważ
![]() . Na mocy tego twierdzenia można
znaleźć takie nieujemne liczby
. Na mocy tego twierdzenia można
znaleźć takie nieujemne liczby
![]() , że dla
funkcji Lagrange'a problemu (
, że dla
funkcji Lagrange'a problemu (![]() )
)
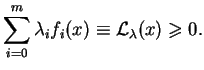
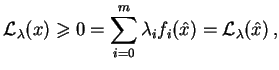
![]() załóżmy, że zachodzi warunek Statera, oraz
załóżmy, że zachodzi warunek Statera, oraz
![]() . Wtedy otrzymujemy, że dla
. Wtedy otrzymujemy, że dla
![]()