



Next: Programowanie dynamiczne problemów ekstremalnych.
Up: Programowanie matematyczne i układy
Previous: Programowanie wypukłe. Zagadnienia związane
Spis rzeczy
Rozważmy problem programowania liniowego
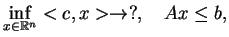 |
(9.1) |
Dualnym problemem PL do (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) nazywa się problem
ekstremalny
) nazywa się problem
ekstremalny
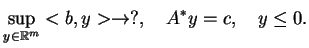 |
(9.2) |
Odpowiednio, dualnym problemem do problemu (gdzie
 )
)
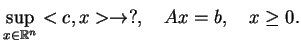 |
(9.3) |
będzie problem ekstremalny
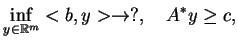 |
(9.4) |
gdzie
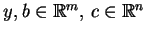 .
.
Najbardziej symetryczne są problemy w postaci normalnej:
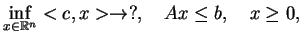 |
(9.5) |
oraz dualny problem do (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) )
)
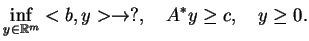 |
(9.6) |
Damy dowód dla (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ).
).
 Włączymy problem (
Włączymy problem (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) w rodzinę problemów PL z parametrem
) w rodzinę problemów PL z parametrem
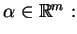
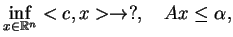 |
(9.7) |
Wartość problemu PL (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) oznaczamy
) oznaczamy
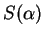 :
:
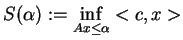 |
(9.8) |
i będziemy nazywać 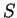 -funkcją problemu
(
-funkcją problemu
(![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ), a
), a 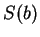 jego poszukiwaną wartością.
jego poszukiwaną wartością.
Dość prosto zobaczyć, że 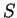 -funkcja (
-funkcja (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) jest wypukła. Jej przekształcenie Fenchel'a oznaczmy
) jest wypukła. Jej przekształcenie Fenchel'a oznaczmy
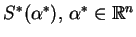 . Wtedy otrzymujemy:
. Wtedy otrzymujemy:
Ponieważ
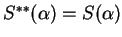 , jeśli
, jeśli
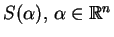 , jest funkcją
domkniętą, znajdujemy z (
, jest funkcją
domkniętą, znajdujemy z (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) że:
) że:
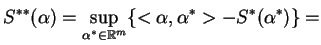 |
(9.10) |
W szczególności,
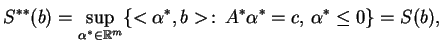 |
(9.11) |
gdy funkcja
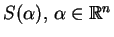 , jest
domknięta. Problem (
, jest
domknięta. Problem (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) jest dualnym do
(
) jest dualnym do
(![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ), jak było wypisane w (
), jak było wypisane w (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ). Z drugiej
strony
). Z drugiej
strony 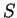 -funkcja (
-funkcja (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) jest domnięta ponieważ
nadwykres funkcji
) jest domnięta ponieważ
nadwykres funkcji 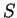 jest zbiorem domkniętym wg. lematu o
domkniętości skończenie zgenerowanego stożka, jakim jest
zbiór
jest zbiorem domkniętym wg. lematu o
domkniętości skończenie zgenerowanego stożka, jakim jest
zbiór
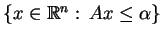
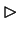
9.1
Uwaga.Podobną metodę można stosować do następnych
trzech podstawowych problemów PL:
- i)
- Zagadnienie ogólne PL:
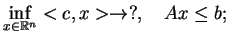 |
(9.12) |
- ii)
- Zagadnienie PL w postaci kanonicznej:
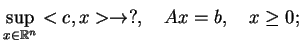 |
(9.13) |
- iii)
- Zagadnienie PL w postaci normalnej:
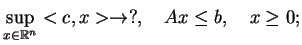 |
(9.14) |
gdzie
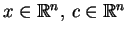 i
i
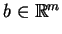
9.2
Uwaga. Jest oczywistym że problem PL (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
)
jest równoważny przy odwzorowaniu
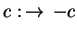
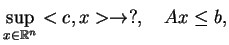 |
(9.15) |
co już był rozważany w rozdziale 6.
9.3
Uwaga. Warunek
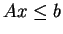
w (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
)
można rozpisać w takiej postaci na mocy definicji
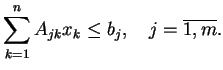 |
(9.16) |
Zdefiniujmy teraz na mocy (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) takie
) takie
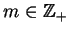 funkcjonałów liniowych na
funkcjonałów liniowych na
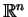 :
:
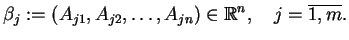 |
(9.17) |
Wtedy oczywiście (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) przyjmie postać zbioru
) przyjmie postać zbioru
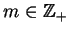 funkcjonałów (
funkcjonałów (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ):
):
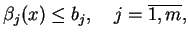 |
(9.18) |
co dokładnie jest to samo co (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ).
).




Next: Programowanie dynamiczne problemów ekstremalnych.
Up: Programowanie matematyczne i układy
Previous: Programowanie wypukłe. Zagadnienia związane
Spis rzeczy
![]() Włączymy problem (
Włączymy problem (![]() ) w rodzinę problemów PL z parametrem
) w rodzinę problemów PL z parametrem
![]()
![]() -funkcja (
-funkcja (![]() ) jest wypukła. Jej przekształcenie Fenchel'a oznaczmy
) jest wypukła. Jej przekształcenie Fenchel'a oznaczmy
![]() . Wtedy otrzymujemy:
. Wtedy otrzymujemy: