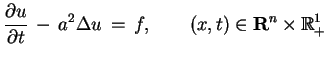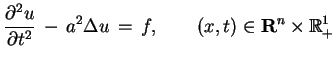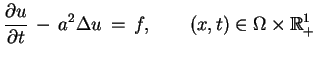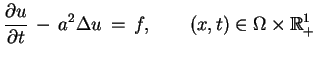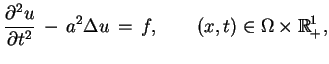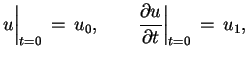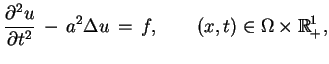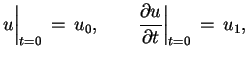Warunki brzegowe oraz początkowe

Jest dość oczywiste, że równanie różniczkowe o pochodnych cząstkowych posiada nie jedno rozwiązanie. Na ogół nie jest możliwe podać ogólne rozwiązanie takiego równania. Tak więc będziemy szukać rozwiązania równania różniczkowego o pochodnych cząstkowych, które spełniają specjalne warunki brzegowe. Przytoczmy kilka przykładów. Niech będzie zadany obszar 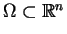$\Omega \subset \mathbb{R}^{n}$ oraz funkcje 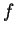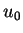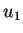$f$, $u_{0}$, $u_{1}$ i $\varphi$.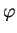
Problem Dirichleta dla równania Laplace'a:

$$\Delta u\,=\,f,\qquad x\in \Omega,$$

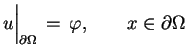$${u}\Big\vert _{\partial \Omega}\,=\,\varphi,\qquad x\in \partial\Omega$$ (6.1)

Problem Neumana dla równania Laplace'a:

$$\Delta u\,=\,f,\qquad x\in \Omega,$$

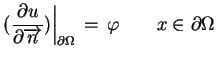$$(\frac{\partial u}{\partial\overrightarrow{n}})\Big\vert _{\partial \Omega}\,=\,\varphi \qquad x \in \partial \Omega$$ (6.2)

Problem Cauchy'ego dla równania przepływu ciepła (rozpowszechnienia ciepła):

$$\frac{\partial u}{\partial t}\,-\,a^{2}\Delta u\,=\,f ,\qquad (x,t)\in \mathbf{R}^{n}\times \mathbb{R}^{1}_{+}$$

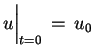$$u \Big \vert _{t=0}\,=\,u_{0}$$ (6.3)

Problem Cauchy'ego dla równania fal:

$$\frac{\partial^{2} u}{\partial t^{2}}\,-\,a^{2}\Delta u \,=\,f, \qquad (x,t)\in \mathbf{R}^{n}\times \mathbb{R}^{1}_{+}$$

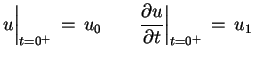$$u \Big \vert _{t=0^{+}}\,=\,u_{0} \qquad \frac{\partial u}{\partial t} \Big \vert _{t=0^{+}}\,=\,u_{1}$$ (6.4)

Pierwszy problem brzegowy dla równania rozpowszechnienia ciepła:

$$\frac{\partial u}{\partial t}\,-\,a^{2}\Delta u \,=\,f, \qquad (x,t)\in \Omega\times \mathbb{R}^{1}_{+}$$

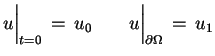$$u \Big \vert _{t=0}\,=\,u_{0} \qquad u \Big \vert _{\partial \Omega}\,=\,u_{1}$$ (6.5)

Drugi problem brzegowy dla równania rozpowszechnienia ciepła:

$$\frac{\partial u}{\partial t}\,-\,a^{2}\Delta u \,=\,f, \qquad (x,t)\in \Omega\times \mathbb{R}^{1}_{+}$$

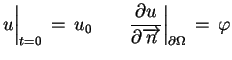$$u \Big \vert _{t=0}\,=\,u_{0} \qquad \frac{\partial u}{\partial \overrightarrow{n}} \Big \vert _{\partial \Omega}\,=\,\varphi$$ (6.6)

Pierwszy problem brzegowy dla równania fal:

$$\frac{\partial^{2} u}{\partial t^{2}}\,-\,a^{2}\Delta u\,=\,f, \qquad (x,t)\in \Omega \times \mathbb{R}^{1}_{+},$$

$$u \Big \vert _{t=0}\,=\,u_{0}, \qquad \frac{\partial u}{\partial t} \Big \vert _{t=0}\,=\,u_{1},$$

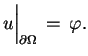$$u \Big \vert _{\partial \Omega}\,=\,\varphi.$$ (6.7)

Drugi problem brzegowy dla równania fal:

$$\frac{\partial^{2} u}{\partial t^{2}}\,-\,a^{2}\Delta u\,=\,f, \qquad (x,t)\in \Omega \times \mathbb{R}^{1}_{+},$$

$$u \Big \vert _{t=0}\,=\,u_{0}, \qquad \frac{\partial u}{\partial t} \Big \vert _{t=0}\,=\,u_{1},$$

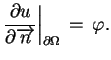$$\frac{\partial u}{\partial \overrightarrow{n}} \Big \vert _{\partial \Omega}\,=\,\varphi.$$ (6.8)

Dla każdego problemu powyżej można podać interpretację fizyczną. Jest bardzo ważnym i subtelnym pytaniem o ilość i charakter tych warunków brzegowych, które mogą gwarantować jednoznaczne rozwiązanie problemu. Takich warunków powinno być nie ''nadto mało'' i nie ''nadto dużo'' żeby rozwiązanie na ogół istniało.