


Next: Klasyfikacja równań quasi-liniowych drugiego
Up: RÓWNANIA FIZYKI MATEMATYCZNEJ
Previous: Warunki brzegowe oraz początkowe
Rozważmy równanie różniczkowe 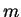 -tego rzędu stosownej
funkcji
-tego rzędu stosownej
funkcji 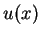 od
od
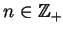 skalarnych zmiennych
skalarnych zmiennych
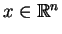 . Klasyfikacja jest bazowana na zależności
równania od pochodych najwyższego rzędu, tj. rzędu
. Klasyfikacja jest bazowana na zależności
równania od pochodych najwyższego rzędu, tj. rzędu 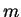 .
Najprostsza sytuacja ma miejsce, kiedy równanie jest
quasi-liniowe, to znaczy najwyźsze pochodne wchodzą w
równanie w sposób liniowy. Takie równania mają postać:
.
Najprostsza sytuacja ma miejsce, kiedy równanie jest
quasi-liniowe, to znaczy najwyźsze pochodne wchodzą w
równanie w sposób liniowy. Takie równania mają postać:
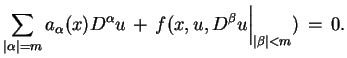 |
(7.1) |
Współczynniki
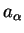 ,
,
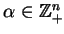 mogą
zależeć od
mogą
zależeć od
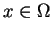 , a wyrażenie
, a wyrażenie 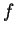 może zależeć od
może zależeć od
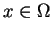 ,
, 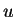 oraz pochodnych
oraz pochodnych
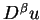 dla
dla 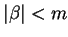 .
Wyrażenie
.
Wyrażenie
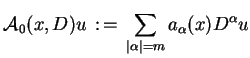 |
(7.2) |
ma nazwę części głównej równania (7.1).
Z wyrażeniem (7.2) można skojarzyć wielomian:
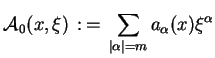 |
(7.3) |
gdzie
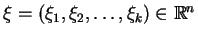 .
Rozważmy równanie algebraiczne:
.
Rozważmy równanie algebraiczne:
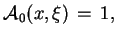 |
(7.4) |
które opisuje powierzchnię w
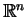 , zależną od
parametru
, zależną od
parametru
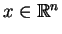 .
.
Subsections



Next: Klasyfikacja równań quasi-liniowych drugiego
Up: RÓWNANIA FIZYKI MATEMATYCZNEJ
Previous: Warunki brzegowe oraz początkowe
Andrzej Janus Szef
2001-12-05
![]() -tego rzędu stosownej
funkcji
-tego rzędu stosownej
funkcji ![]() od
od
![]() skalarnych zmiennych
skalarnych zmiennych
![]() . Klasyfikacja jest bazowana na zależności
równania od pochodych najwyższego rzędu, tj. rzędu
. Klasyfikacja jest bazowana na zależności
równania od pochodych najwyższego rzędu, tj. rzędu ![]() .
Najprostsza sytuacja ma miejsce, kiedy równanie jest
quasi-liniowe, to znaczy najwyźsze pochodne wchodzą w
równanie w sposób liniowy. Takie równania mają postać:
.
Najprostsza sytuacja ma miejsce, kiedy równanie jest
quasi-liniowe, to znaczy najwyźsze pochodne wchodzą w
równanie w sposób liniowy. Takie równania mają postać: