Definicja 7.1
Niech punkt
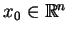
jest ustalony. Jeśli
istnieje taka liczba
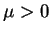
, że
dla wszystkich
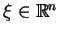
, to równanie
(
7.1) ma typ eliptyczny; jeśli wszystkie wartości
własne macierzy
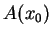
są niezerowe i jednego znaku oprócz
jednego, którego znak jest przeciwny, to równanie
(
7.1) jest typu hiperbolicznego; jeśli wszystkie
wartości własne macierzy
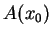
oprócz jednego są
niezerowe i jednego znaku, wtedy równanie (
7.1) jest
typu parabolicznego.
![]() wielomian (7.3) ma postać formy
kwadratowej:
wielomian (7.3) ma postać formy
kwadratowej:
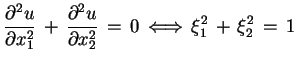
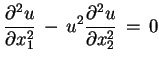
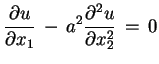
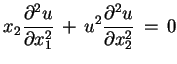
![]() mamy
następujące definicje:
mamy
następujące definicje: