


Next: Problem Cauchy'ego dla równań
Up: Klasyfikacja równań o pochodnych
Previous: Klasyfikacja równań quasi-liniowych drugiego
Rozważmy hiperpowierzchnię
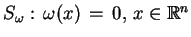 , gdzie
, gdzie
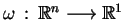 jest różniczkowalnym odwzorowaniem w otoczeniu
powierzchni
jest różniczkowalnym odwzorowaniem w otoczeniu
powierzchni
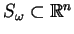 . Powierzchnię
. Powierzchnię
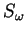 nazywamy charakterystychną dla równania
(7.1) jeśli spełniona na
nazywamy charakterystychną dla równania
(7.1) jeśli spełniona na
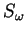 jest
następująca równość:
jest
następująca równość:
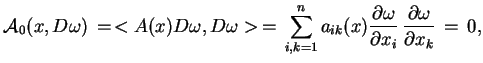 |
(7.10) |
gdzie
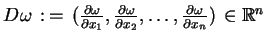 nazywa się gradientem odwzorowania
nazywa się gradientem odwzorowania
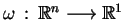 . Mamy
następującą interpretację geometryczną powierzchni
charakterystycznej. Mianowicie, ponieważ gradient
. Mamy
następującą interpretację geometryczną powierzchni
charakterystycznej. Mianowicie, ponieważ gradient
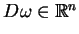 jako wektor jest prostopadły w każdym punkcie
jako wektor jest prostopadły w każdym punkcie
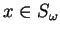 , to warunek (7.10) znaczy, że pole
wektorowe w
, to warunek (7.10) znaczy, że pole
wektorowe w
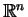
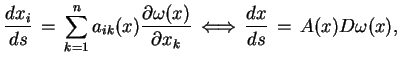 |
(7.11) |
gdzie
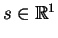 jest parametrem ewolucji, jest
styczne do powierzchni
jest parametrem ewolucji, jest
styczne do powierzchni
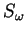 , tj.
, tj.
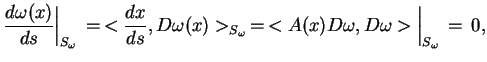 |
(7.12) |
co jest równoważne prostopadłości pola wektorowego
(7.11) wektora gradientu
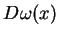 na
na
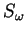 .
.
Rozważmy teraz równanie (7.1) przy
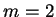 , i zastosujmy przekształcenie
, i zastosujmy przekształcenie
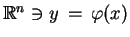 , gdzie
, gdzie
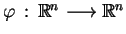 jest
różniczkowalnym z niezdegenerowanym Jakobianem, tj.
jest
różniczkowalnym z niezdegenerowanym Jakobianem, tj.
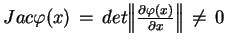 , do równania (7.1) w postaci
, do równania (7.1) w postaci
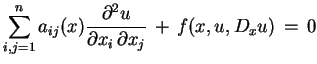 |
(7.13) |
Jako wynik otrzymujemy, że (7.13) przetwarza się w
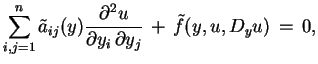 |
(7.14) |
gdzie
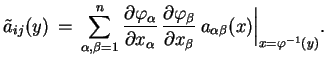 |
(7.15) |
na mocy tego, że
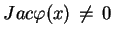 typ równania
(7.13) pozostaje niezmiennym. To znaczy, że można tak
dobrać odwzorowanie
typ równania
(7.13) pozostaje niezmiennym. To znaczy, że można tak
dobrać odwzorowanie
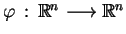 , żeby macierz
, żeby macierz
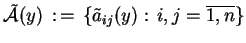 była prostszej
postaci.
była prostszej
postaci.
Rozważmy bardziej dokładnie przypadek 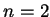 . W tym przypadku
zbadamy charakterystyki równania (7.13) (przy
. W tym przypadku
zbadamy charakterystyki równania (7.13) (przy 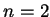 ):
):
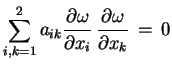 |
(7.16) |
lub
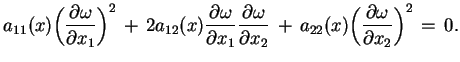 |
(7.17) |
Wyrażenie (7.17) można przekształcić do takiej
postaci:
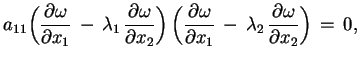 |
(7.18) |
gdzie
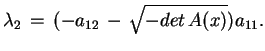 |
(7.19) |
Niech
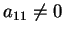 ; wtedy równanie
; wtedy równanie
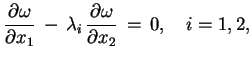 |
(7.20) |
równoważne jest polom wektorowym
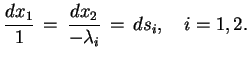 |
(7.21) |
To znaczy, że równanie
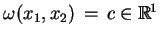 jest niezmiennikiem pól wektorowych
(7.21). Znajdując
jest niezmiennikiem pól wektorowych
(7.21). Znajdując
 z
(7.21) i podstawiając je w (7.18)
otrzymujemy:
z
(7.21) i podstawiając je w (7.18)
otrzymujemy:
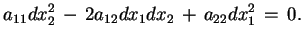 |
(7.22) |
Tym samym udowodniliśmy twierdzenie:
Twierdzenie 7.2
Charakterystyki równania (
7.13) przy
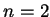
są
rozwiązaniem formy różniczkowo-kwadratowej (
7.22)
lub formy (
7.21).
Niech teraz odwzorowanie
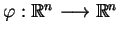 wprowadzone wyżej, ma następującą postać:
wprowadzone wyżej, ma następującą postać:
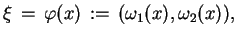 |
(7.23) |
gdzie
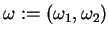 są dwoma
charakterystykami równania (7.13) jako rozwiązania
(7.22).
Niech równanie (7.13) będzie eliptycznym. Wtedy mamy
dwie charakterystyki
są dwoma
charakterystykami równania (7.13) jako rozwiązania
(7.22).
Niech równanie (7.13) będzie eliptycznym. Wtedy mamy
dwie charakterystyki
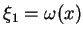 i
i
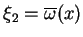 sprzężone nawzajem. Wprowadzając
nowe zmienne
sprzężone nawzajem. Wprowadzając
nowe zmienne
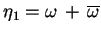 oraz
oraz
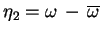 , będące już
rzeczywistymi, oraz wykorzystując (7.15) otrzymujemy,
że równanie (7.14) (przy
, będące już
rzeczywistymi, oraz wykorzystując (7.15) otrzymujemy,
że równanie (7.14) (przy 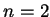 ) przyjmuje postać:
) przyjmuje postać:
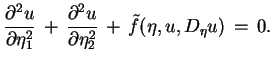 |
(7.24) |
W analogiczny sposób otrzymujemy dla równania (7.13)
parabolicznego, że jego postać kanoniczna (7.14) jest
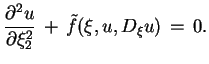 |
(7.25) |
W przypadku, gdy równanie (7.13) jest hiperboliczne
znajdujemy, stosując odwzorowanie
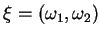 ,
takie że (7.14) daje wyrażenie kanoniczne
,
takie że (7.14) daje wyrażenie kanoniczne
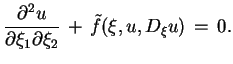 |
(7.26) |



Next: Problem Cauchy'ego dla równań
Up: Klasyfikacja równań o pochodnych
Previous: Klasyfikacja równań quasi-liniowych drugiego
Andrzej Janus Szef
2001-12-05
![]() , gdzie
, gdzie
![]() jest różniczkowalnym odwzorowaniem w otoczeniu
powierzchni
jest różniczkowalnym odwzorowaniem w otoczeniu
powierzchni
![]() . Powierzchnię
. Powierzchnię
![]() nazywamy charakterystychną dla równania
(7.1) jeśli spełniona na
nazywamy charakterystychną dla równania
(7.1) jeśli spełniona na
![]() jest
następująca równość:
jest
następująca równość:
![]() , i zastosujmy przekształcenie
, i zastosujmy przekształcenie
![]() , gdzie
, gdzie
![]() jest
różniczkowalnym z niezdegenerowanym Jakobianem, tj.
jest
różniczkowalnym z niezdegenerowanym Jakobianem, tj.
![]() , do równania (7.1) w postaci
, do równania (7.1) w postaci
![]() . W tym przypadku
zbadamy charakterystyki równania (7.13) (przy
. W tym przypadku
zbadamy charakterystyki równania (7.13) (przy ![]() ):
):
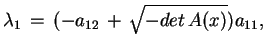
![]() wprowadzone wyżej, ma następującą postać:
wprowadzone wyżej, ma następującą postać: