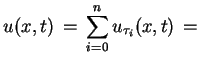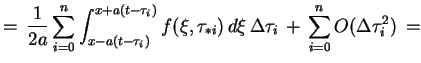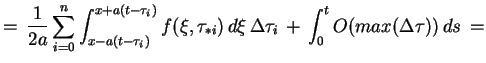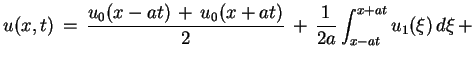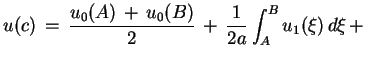Next: Problemy Cauchy'ego i Gaursat'a
Up: Problem Cauchy'ego dla równań
Previous: Problem Cauchy'ego dla równań
Rozważmy następujący problem: odzyskać funkcję
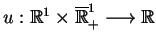 , spełniającą równania hiperboliczne
, spełniającą równania hiperboliczne
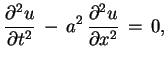 |
(8.1) |
oraz warunki początkowe :
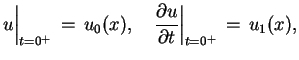 |
(8.2) |
gdzie
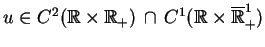 .
.
Charakterystykami równania (8.1) są
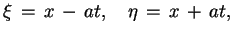 |
(8.3) |
otrzymujemy z (7.26), że
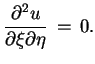 |
(8.4) |
Z (8.3) mamy, że
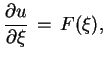 |
(8.5) |
gdzie
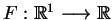 jest pewną
funkcją. Całkując (8.5) po
jest pewną
funkcją. Całkując (8.5) po
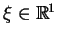 ,
otrzymujemy, że
,
otrzymujemy, że
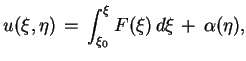 |
(8.6) |
gdzie
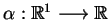 jest też
pewną jeszcze niewiadomą funkcją. Wykorzystując teraz
odwzorowanie (8.3), z (8.5) znajdujemy, że
jest też
pewną jeszcze niewiadomą funkcją. Wykorzystując teraz
odwzorowanie (8.3), z (8.5) znajdujemy, że
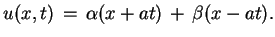 |
(8.7) |
gdzie
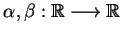 są
pewnymi funkcjami, które znajdujemy wykorzystując warunki
początkowe (8.2). Mianowicie
są
pewnymi funkcjami, które znajdujemy wykorzystując warunki
początkowe (8.2). Mianowicie
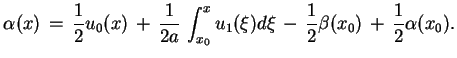 |
(8.8) |
Podstawiając (8.8) w (8.7), znajdujemy że
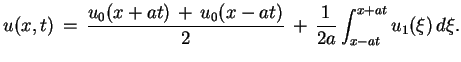 |
(8.9) |
Wzór (8.9) nosi nazwę wzoru d'Alamberta, i daje
rozwiązanie problemu (8.1), (8.2) w postaci
dokładej.
Rozważmy teraz przypadek równania niejednorodnego:
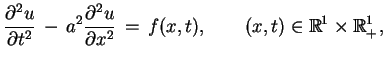 |
(8.10) |
z warunkami Cauchy'ego
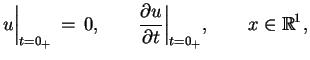 |
(8.11) |
gdzie
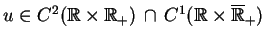 .
.
Równanie (8.10) opisuje poruszanie nieskończonej
struny pod
zewnętrznym działaniem sił zaburzenia.
Dla rozwiązania równania (8.10) rozważmy
stowarzyszony z (8.10) problem
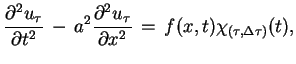 |
(8.12) |
gdzie
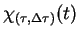 jest funkcją indykatorową
(lub wskaźnikową) otwartego przedziału
jest funkcją indykatorową
(lub wskaźnikową) otwartego przedziału
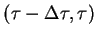 ,
,
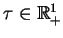 ,
,
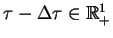 :
:
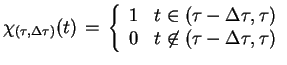 |
(8.13) |
funkcja
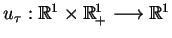 z ineksem
z ineksem
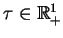 spełnia warunek Cauchy'ego
spełnia warunek Cauchy'ego
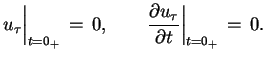 |
(8.14) |
Ponieważ zaburzenie
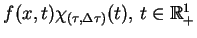 jest dla
jest dla
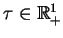 niezerowym tylko dla
niezerowym tylko dla
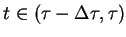 , to dla
wszystkich
, to dla
wszystkich
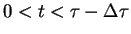 rozwiązanie
rozwiązanie
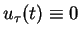 , co zachodzi z (8.9) i (8.14).
, co zachodzi z (8.9) i (8.14).
Niech teraz zmienna
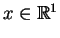 jest traktowana jako
parametr. Wtedy równanie (8.12) może być przepisane w
takiej postaci:
jest traktowana jako
parametr. Wtedy równanie (8.12) może być przepisane w
takiej postaci:
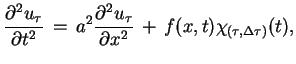 |
(8.15) |
z warunkami (8.14). Ponieważ prawa część
(8.15) jest funkcją ciągłą dla
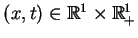 , można wypisać jego
rozwiązanie w postaci uwikłanej:
, można wypisać jego
rozwiązanie w postaci uwikłanej:
![$\displaystyle =\,\frac{1}{a}\sin\,a(\tau-\tau^{*})\Big[a^{2}\frac{
\partial^{2}u_{\tau}(x,\tau^{*})}{\partial
x^{2}}\,+\,f(x,\tau^{*})\Big]\,\Delta\tau$](img726.gif) |
(8.16) |
dla pewnego
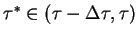 , co zachodzi na
mocy 1 twierdzenia o średniej wartości całki. Ponieważ
, co zachodzi na
mocy 1 twierdzenia o średniej wartości całki. Ponieważ
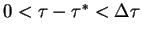 , przyjmując że
, przyjmując że
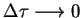 jednostajnie po
jednostajnie po
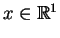 z (8.16) wnioskujemy, że
z (8.16) wnioskujemy, że
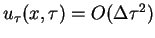 , tj. z dokładnością
, tj. z dokładnością
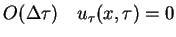 . Wsposób całkiem
analogiczny znajdujemy, że
. Wsposób całkiem
analogiczny znajdujemy, że
![$\displaystyle \frac{\partial u_{\tau}(x,t)}{\partial t}\,
=\,\int^{t}_{0}\cos\...
...u_{\tau}(x,s)}{\partial
x^{2} }\,+\,f(x,s)\chi_{(\tau,\Delta\tau)}(s)\Big]\,ds$](img732.gif) |
(8.17) |
dla wszystkich
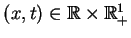 skąd przy
skąd przy 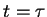 zachodzi
zachodzi
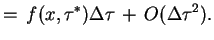 |
(8.18) |
gdzie
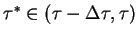 .
.
W taki sposób zredukowaliśmy problem (8.12) do
problemu znalezienia funkcji
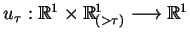 , która
spełnia równanie jednorodne
, która
spełnia równanie jednorodne
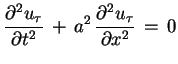 |
(8.19) |
oraz warunki początkowe przy 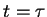 :
:
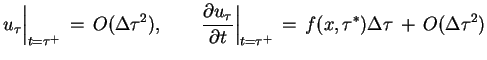 |
(8.20) |
przy
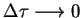 . Korzystając teraz ze wzoru
d'Alamberta (8.6), zapisujemy rozwiązania problemu
(8.19) i (8.20):
. Korzystając teraz ze wzoru
d'Alamberta (8.6), zapisujemy rozwiązania problemu
(8.19) i (8.20):
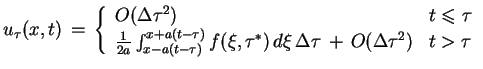 |
(8.21) |
Teraz wróćmy do problemu (8.10) i
(8.11), zapisując odwzorowanie
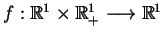 w takiej postaci:
w takiej postaci:
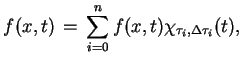 |
(8.22) |
gdzie oczywiście
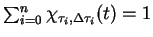 dla każdego
dla każdego
 , jeśli
, jeśli
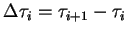 ,
,
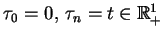 . Tak więc mamy
problem Cauchy'ego:
. Tak więc mamy
problem Cauchy'ego:
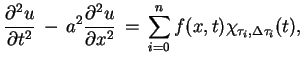 |
(8.23) |
oraz
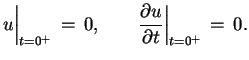 |
(8.24) |
Ponieważ równanie (8.23) jest liniowe niejednorodne z
jednorodnymi warunkami Cauchy'ego (8.24), jego
rozwiązanie jest sumą rozwiązań poszczególnych problemów
(8.12), (8.14). Tak więc mamy na mocy
wyrażenia (8.21) następujące rozwiązanie
(8.10):
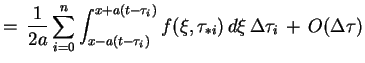 |
(8.25) |
Biorąc teraz granice (8.25) przy
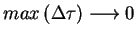 , otrzymujemy że
, otrzymujemy że
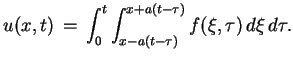 |
(8.26) |
Rozważmy teraz ogólny problem Cauchy'ego w takiej postaci:
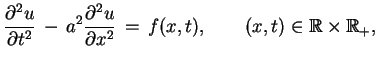 |
(8.27) |
gdzie
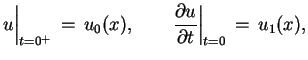 |
(8.28) |
oraz
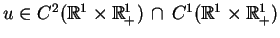 .
.
Rozwiązanie problemu (8.27) i (8.28)
można łatwo otrzymać, kojarząc problemy Cauchy'ego
(8.10), (8.11) i (8.1),
(8.2):
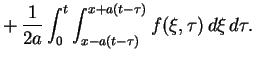 |
(8.29) |
Uwaga 8.1
Trójkąt charakterystyk i rozwiązania (
8.29).
Rozważmy na płaszczyźnie
 trójkąt ABC:
trójkąt ABC:
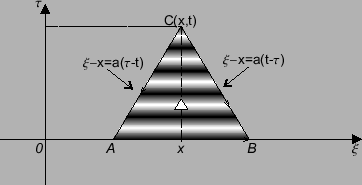
Rys. 4
|
Wtedy rozwiązanie (8.29) przyjmuje następującą
postać:
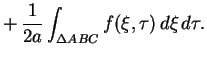 |
(8.30) |



Next: Problemy Cauchy'ego i Gaursat'a
Up: Problem Cauchy'ego dla równań
Previous: Problem Cauchy'ego dla równań
Andrzej Janus Szef
2001-12-05
![]() , spełniającą równania hiperboliczne
, spełniającą równania hiperboliczne
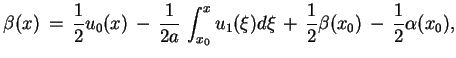
![]() jest traktowana jako
parametr. Wtedy równanie (8.12) może być przepisane w
takiej postaci:
jest traktowana jako
parametr. Wtedy równanie (8.12) może być przepisane w
takiej postaci:
![$\displaystyle u_{\tau}(x,\tau)\,=\,\frac{1}{a}\int^{\tau}_{0}\sin\,a(\tau-s)\Bi...
..._{\tau}(x,s)}{\partial
x^{2}}\,+\,f(x,s)\chi(\tau,\Delta\tau)(s)\Big]\,ds\,=
$](img723.gif)
![$\displaystyle =\,\frac{1}{a}\int^{\tau-\Delta\tau}_{0}\sin\,a(\tau-s)\Big[a^{2}...
...x,s)}{\partial
x^{2}}}_{0}\,+\,f(x,s)\cdot0\Big]\Big\vert _{u_{\tau}=0}ds\,+
$](img724.gif)
![$\displaystyle +\,\frac{1}{a}\int^{\tau}_{\tau-\Delta\tau}\sin\,a(\tau-s)\Big[a^{2}\frac{
\partial^{2}u_{\tau}(x,s)}{\partial x^{2}}\,+\,f(x,s)\Big]\,ds\,=
$](img725.gif)
![$\displaystyle \frac{\partial u_{\tau}(x,t)}{\partial t}\,
=\,\int^{\tau-\Delta...
...x,s)}{\partial
x^{2} }\,+\,f(x,s)\cdot 0\Big]\Big\vert _{u_{\tau}=0}\,ds \,+
$](img735.gif)
![$\displaystyle +\,\int_{\tau-\Delta\tau}^{\tau}\cos\,a(t-s)\Big[a^{2}\frac{\partial^{2}u_{\tau}(x,s)}{\partial
x^{2} }\,+\,f(x,s)\Big]\,ds \,=
$](img736.gif)
![]() , która
spełnia równanie jednorodne
, która
spełnia równanie jednorodne
![]() w takiej postaci:
w takiej postaci: