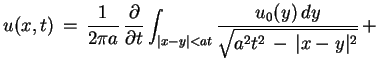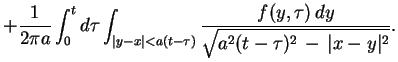Next: Twierdzenie Cauchy'ego-Kowalewskiej
Up: Problem Cauchy'ego dla trójwymiarowego
Previous: Problem Cauchy'ego w dla
Rozważmy problem Cauchy'ego w
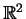 :
:
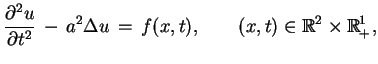 |
(9.22) |
gdzie
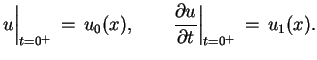 |
(9.23) |
Dla rozwiązania (9.22), (9.23) rozważmy
wspomagający problem Cauchy'ego w
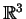 , gdzie funkcje
, gdzie funkcje
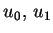 oraz
oraz 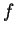 nie zależą od zmiennej
nie zależą od zmiennej
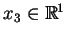 . Wtedy rozwiązanie tego problemu już mamy:
. Wtedy rozwiązanie tego problemu już mamy:
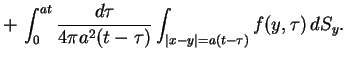 |
(9.24) |
Ponieważ podcałkowe funkcje nie zależą od
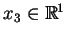 , to całkowanie po sferze zamienimy całkowaniem
po kole o dużej średnicy, które jest przecięciem sfery
płaszczyzną
, to całkowanie po sferze zamienimy całkowaniem
po kole o dużej średnicy, które jest przecięciem sfery
płaszczyzną 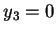 .
.
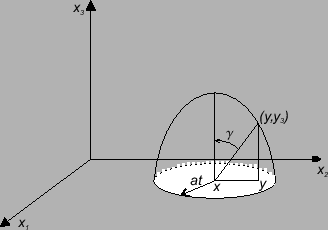
Rys. 6
|
Mamy:
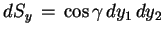 ,
,
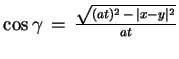 , gdzie
, gdzie
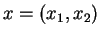 ,
,
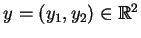 .
.
Teraz całka
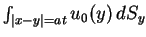 w (9.24)
będzie się równać całce
w (9.24)
będzie się równać całce
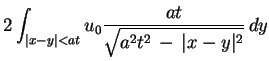 |
(9.25) |
(współczynnik ,,2'' odpowiada za całkowanie po dwóch
połówkach sfery). Wykonajmy analogiczne przekształcenia we
wszystkich całkach (9.24), znajdujemy:
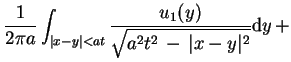 |
(9.26) |
Wzór (9.26) podał Poisson, który wyprowadził go w
sposób całkiem podobny jak stosowany powyżej i który ma nazwę
metody redukcji po zmiennej przestrzennej.



Next: Twierdzenie Cauchy'ego-Kowalewskiej
Up: Problem Cauchy'ego dla trójwymiarowego
Previous: Problem Cauchy'ego w dla
Andrzej Janus Szef
2001-12-05
![]() :
:
![]() , gdzie funkcje
, gdzie funkcje
![]() oraz
oraz ![]() nie zależą od zmiennej
nie zależą od zmiennej
![]() . Wtedy rozwiązanie tego problemu już mamy:
. Wtedy rozwiązanie tego problemu już mamy:
![$\displaystyle u(x,t)\,=\,\frac{\partial}{\partial t}\Big[\frac{1}{4\pi a^{2}t}
...
... \Big]\,+\,\frac{1}{4\pi a^{2}
t}\int_{\vert x-y\vert=at}u_{1}(y)\,dS_{y}\,+
$](img948.gif)

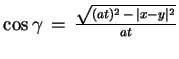 , gdzie
, gdzie