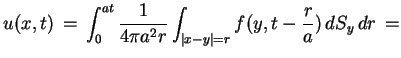Next: Problem Cauchy'ego w dla
Up: Problem Cauchy'ego dla trójwymiarowego
Previous: Średnie kuliste
Rozważmy równanie
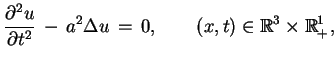 |
(9.9) |
gdzie
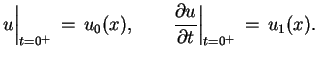 |
(9.10) |
Żeby rozwiązać równanie (9.9) z warunkami
(9.10) stosujemy uśrednienie kuliste do równania
(9.9), ( ):
):
![$\displaystyle \frac{\partial^{2}\overline{u}}{\partial t^{2}}\,-\,a^{2}\Big[
\...
... r^{2}}\,+\,\frac{2}{r}\,\frac{\partial \overline{u}}{\partial r}
\Big]\,=\,0.$](img911.gif) |
(9.11) |
Mnożąc (9.11) przez
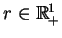 sprowadzamy (9.11) do postaci
sprowadzamy (9.11) do postaci
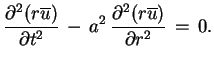 |
(9.12) |
Równanie (9.12) jest już jednowymiarowym równaniem
falowym dla funkcji
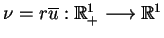 . Odpowiednie u"srednienie warunków początkowych
(9.10) daje:
. Odpowiednie u"srednienie warunków początkowych
(9.10) daje:
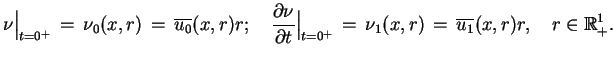 |
(9.13) |
Ponieważ funkcja
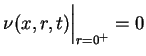 , rozwiązanie
równania (9.12) może być przedłużone na całą oś
, rozwiązanie
równania (9.12) może być przedłużone na całą oś
 nieparzystym sposobem. To znaczy, że warunki
początkowe
nieparzystym sposobem. To znaczy, że warunki
początkowe
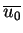 i
i
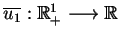 mają być przedłuźone na ujemną oś
mają być przedłuźone na ujemną oś
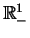 parzystym sposobem. Wtedy oczywiście stosując wzór
d'Alemberta (8.9) znajdujemy, że
parzystym sposobem. Wtedy oczywiście stosując wzór
d'Alemberta (8.9) znajdujemy, że
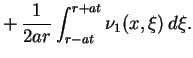 |
(9.14) |
Żeby znaleźć 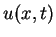 obliczymy granicę (9.14) przy
obliczymy granicę (9.14) przy
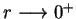 . Ponieważ funkcje
. Ponieważ funkcje 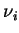 ,
, 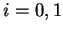 są
nieparzyste wg zmiennej
są
nieparzyste wg zmiennej
 , to mamy
nieokreśloność
, to mamy
nieokreśloność
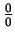 . Stosując prawo de
l'Hospitala znajdujemy:
. Stosując prawo de
l'Hospitala znajdujemy:
![$\displaystyle u(x,t)\,=\,\frac{\nu_{0}^{'}(x,at)\,+\,\nu_{0}^{'}(x,-at)}{2}\,+\,\frac{1}{2a}
\big[\nu_{1}(x,at)\,-\,\nu_{1}(x,-at)\big].$](img928.gif) |
(9.15) |
Ponieważ funkcja 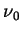 jest nieparzysta to funkcja
jest nieparzysta to funkcja
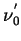 jest parzysta. Wówczas otrzymujemy:
albo
jest parzysta. Wówczas otrzymujemy:
albo
![$\displaystyle u(x,t)\,=\,\frac{\partial}{\partial t}\Big[ \frac{1}{4\pi
a^{2}t...
...dS_{y}\Big]\,+\,\frac{1}{4\pi
a^{2}t}\int_{\vert y-x\vert=at}u_{1}(y)\,dS_{y}.$](img932.gif) |
(9.16) |
Wzór (9.16) ma nazwę wzoru Kirchoff'a. Żeby
rozwiązanie (9.16) było klasycznym dla problemu
Cauchy'ego (9.9), (9.10), jest koniecznym
żeby funkcje
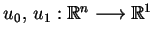 spełniały następujące warunki:
spełniały następujące warunki:
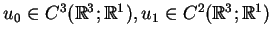 . Jest oczywistym, że
rozwiązanie klasyczne jest jedyne, oraz istnieje ciągła
zależność rozwiązania od warunków początkowych.
. Jest oczywistym, że
rozwiązanie klasyczne jest jedyne, oraz istnieje ciągła
zależność rozwiązania od warunków początkowych.
Rozważmy teraz problem Cauchy'ego dla równania
niejednorodnego
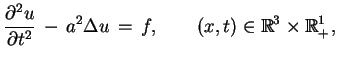 |
(9.17) |
gdzie
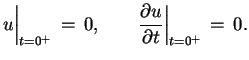 |
(9.18) |
Dla rozwiązania skorzystamy z taj samej metody co wyżej dla
równania (8.10). Tak więc dla rozwiązania
(9.17) i (9.18) mamy zgodnie z
(9.16) następujące wyrażenie:
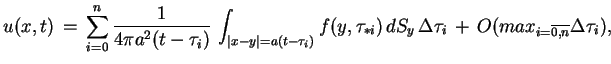 |
(9.19) |
gdzie
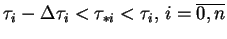 .
.
Biorąc granicę gdy
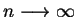 oraz
oraz
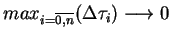 , z (9.19) otrzymujemy, że
, z (9.19) otrzymujemy, że
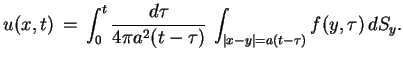 |
(9.20) |
Wyrażenie (9.20) ma nazwę potencjału
opóźniającego. Żeby ten termin uzasadnić wykonamy
następujące przekształcenia :
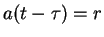 ,
,
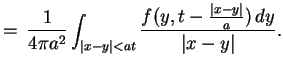 |
(9.21) |
W zwykły sposób sumując rozwiązania (9.20) oraz
(9.16) otrzymujemy rozwiązanie problemu Cauchy'ego
dla równania (9.17) z warunkami początkowymi
(9.10).



Next: Problem Cauchy'ego w dla
Up: Problem Cauchy'ego dla trójwymiarowego
Previous: Średnie kuliste
Andrzej Janus Szef
2001-12-05
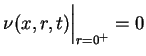 , rozwiązanie
równania (9.12) może być przedłużone na całą oś
, rozwiązanie
równania (9.12) może być przedłużone na całą oś
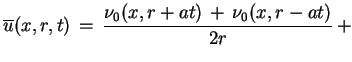
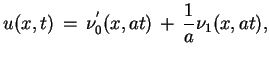
![]() oraz
oraz
![]() , z (9.19) otrzymujemy, że
, z (9.19) otrzymujemy, że