


Next: Własności wartości własnych i
Up: Problemy brzegowe dla równań
Previous: Wzory Green'a.
Lemat 12.1
Niech
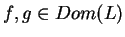
. Wtedy
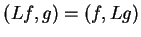 |
(12.7) |
gdzie
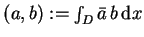
- iloczyn skalarny w
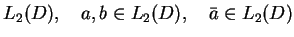
-
sprzężenie zespolone.
Mamy na mocy (12.6), że
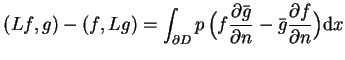 |
(12.8) |
gdzie
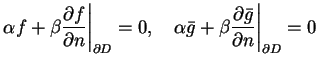 |
(12.9) |
Ponieważ na
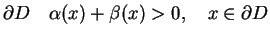 , to wyznacznik
, to wyznacznik
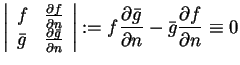 |
(12.10) |
co gwarantuje warunek
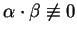 . Teraz
podstawiając (12.10) w (12.8) znajdujemy
(12.7)
. Teraz
podstawiając (12.10) w (12.8) znajdujemy
(12.7)
Połóżmy teraz w (12.5) 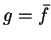 gdzie
gdzie
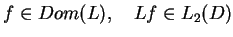 :
:
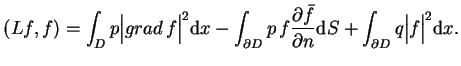 |
(12.11) |
Korzystając z (12.2), tj.
znajdujemy z (12.11), że dla
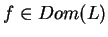
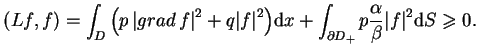 |
(12.12) |
Forma kwadratowa (12.12) ma nazwe całki energii. Niech
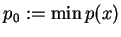 .
.
Ponieważ 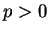 na
na 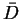 , z tego że
, z tego że
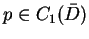 otrzymujemy, że
otrzymujemy, że 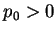 . Tak więc z
(12.12) otrzymujemy takie oszacowanie:
. Tak więc z
(12.12) otrzymujemy takie oszacowanie:
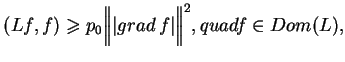 |
(12.13) |
tj. operator
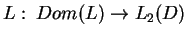 jest dodatni. Z
tego, że
jest dodatni. Z
tego, że
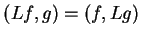 wnioskujemy, że operator
wnioskujemy, że operator 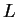 jest
hermitowski.
jest
hermitowski.



Next: Własności wartości własnych i
Up: Problemy brzegowe dla równań
Previous: Wzory Green'a.
Andrzej Janus Szef
2001-12-05
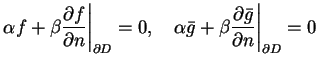
![]() gdzie
gdzie
![]() :
:
