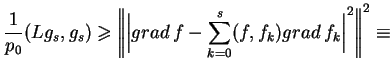Next: Problem Sturma-Liouville'a na
Up: Problemy brzegowe dla równań
Previous: Własności operatora
Twierdzenie 12.2
Wszystkie wartości własne operatora
są dodatnie.
Dowód jest bazowany na nierówności (12.13)
Twierdzenie 12.3
Funkcje własne mogą być wybrane rzezywistymi
Dowód jest bazowany na rzeczywistości operatora
 .
.
Rozważmy teraz przypadek gdy
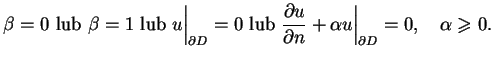 |
(12.14) |
Wtedy zachodzi takie twierdzenie:
Twierdzenie 12.4
Zbiór wartości własnych
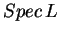
operatora
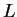
jest
przeliczalny i nie ma skończonych punktów granicznych; każda
wartość własna ma skończoną krotność. Każda funkcja z
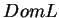
ma rozwinięcie w regularno zbieżny szereg Fourier'a po
funkcjach operatora
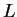
.
Niech
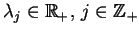 ,
są wartościami własnymi operatora
,
są wartościami własnymi operatora
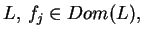
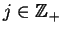 jego odpowiednimi funkcjami
własnymi, tj.
jego odpowiednimi funkcjami
własnymi, tj.
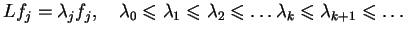 |
(12.15) |
Funkcje własne
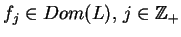 mogą
być wybrane ortogonalne i ortonormowane, tj.
mogą
być wybrane ortogonalne i ortonormowane, tj.
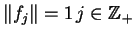 , oraz
, oraz
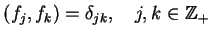 |
(12.16) |
Niech teraz
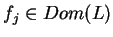 . Na mocy Tw(12.4) mamy
rozwinięcie w szereg Fourier'a:
. Na mocy Tw(12.4) mamy
rozwinięcie w szereg Fourier'a:
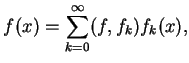 |
(12.17) |
przy czym szereg (12.17) jest zbieżny regularnie w
 . Z drugiej strony, jest oczywistym, że przestrzeń
. Z drugiej strony, jest oczywistym, że przestrzeń
 . Ponieważ
. Ponieważ
 , tj.
, tj.
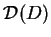 jest
gęsta w
jest
gęsta w 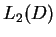 , otrzymujemy że
, otrzymujemy że
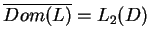 ,
tj.
,
tj. 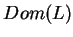 jest gęsta w
jest gęsta w 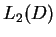 . Stąd zachodzi
. Stąd zachodzi
Rozważmy teraz wyrażenie dla
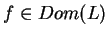 :
:
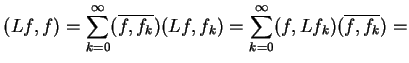 |
|
|
(12.18) |
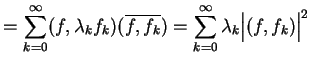 |
|
|
|
Niech
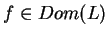 oraz
oraz
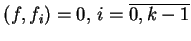 .
Wtedy z (12.18) mamy:
.
Wtedy z (12.18) mamy:
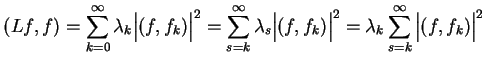 |
(12.20) |
Z drugiej strony mamy równość Parsewala:
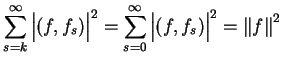 |
(12.21) |
Teraz korzystając z (12.21) i (12.20)
znajdujemy:
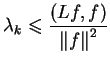 |
(12.22) |
Biorąc 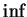 z prawej strony wyrażenia (12.22)
otrzymujemy:
z prawej strony wyrażenia (12.22)
otrzymujemy:
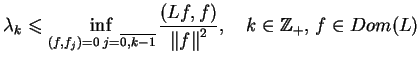 |
(12.23) |
Z drugiej strony przy
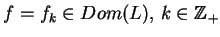 z (12.20) otrzymujemy, że
z (12.20) otrzymujemy, że
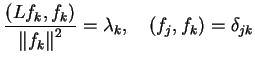 |
(12.24) |
tj. infimum w (12.23) jest osiągalne. Tak więc
zachodzi równość (12.19)
Niech taraz
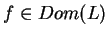 i
i
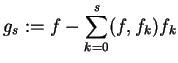 |
(12.25) |
dla
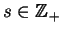 . Stosując (12.18) do
(12.25) otrzymujemy:
. Stosując (12.18) do
(12.25) otrzymujemy:
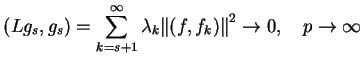 |
(12.26) |
ponieważ szereg (12.18) jest zbieżny.
Na mocy teraz nierówności (12.13) z (12.26)
zachodzi:
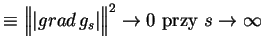 |
(12.27) |
Tak więc otrzymaliśmy równość w 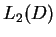
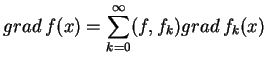 |
(12.28) |
tj. na mocy (12.27) szereg (12.28) jest
zbieżny po normie 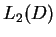 do funkcji
do funkcji
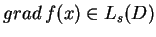 co dowodzi twierdzenie poniżej
co dowodzi twierdzenie poniżej
Twierdzenie 12.7
Niech
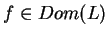
; wtedy szereg Fourier'a (
12.17)
można różniczkować po
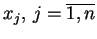
jeden raz i
szeregi otrzymane będą
zbieżne do
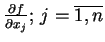
odpowiednio po normie przestrzeni
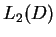



Next: Problem Sturma-Liouville'a na
Up: Problemy brzegowe dla równań
Previous: Własności operatora
Andrzej Janus Szef
2001-12-05
![]() i
i