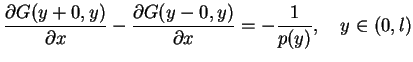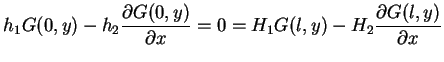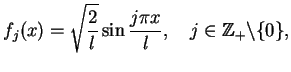Next: Funkcje Bessel'a
Up: Problem Sturma-Liouville'a na
Previous: Problem Sturma-Liouville'a na
Niech
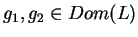 są rozwiązaniami
(13.1) przy
są rozwiązaniami
(13.1) przy 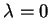 z takimi warunkami brzegowymi:
z takimi warunkami brzegowymi:
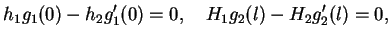 |
(13.3) |
Na mocy twierdzęn z teorii równań różniczkowych zwyczajnych
znajdujemy że
![$ g_{1},g_{2} \in C^2([0,l])$](img1548.gif) i jako rozwiązania
(13.1), (13.1) istnieją przy
i jako rozwiązania
(13.1), (13.1) istnieją przy
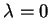 . Oczywiście że rozwiązania
. Oczywiście że rozwiązania
![$ g_{1},g_{2} \in C^2([0,l])$](img1548.gif) są liniowo niezależne ponieważ
są liniowo niezależne ponieważ 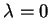 nie jest
wartością własną operatora
nie jest
wartością własną operatora 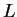 . To znaczy także że zachodzi
tożsamość Ostrogradskiego-Liouville'a:
gdzie
. To znaczy także że zachodzi
tożsamość Ostrogradskiego-Liouville'a:
gdzie
![$\displaystyle w(x):= det \left[ \begin{array}{cc}
g_{1}(x) & g_{2}(x)\\
g'_{1}(x)& g'_{2}(x)
\end{array}
\right]$](img1550.gif) |
(13.4) |
dla
![$ x \in [0,l]$](img1551.gif) . Będziemy teraz szukać rozwiązania w postaci
. Będziemy teraz szukać rozwiązania w postaci
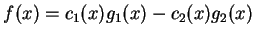 |
(13.5) |
stosując metodę uzmienniania stałych. Jako wynik mamy:
![$\displaystyle f(x)=-\frac{1}{p(x)w(x)}\Big[ g_{2}(x) \int_{0}^{x}r(y)g_{1}(y)
\mathrm{d}y +g_{1}(x) \int_{x}^{l}r(y)g_{2}(y) \mathrm{d}y\Big]$](img1553.gif) |
(13.6) |
albo
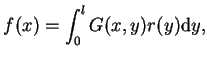 |
(13.7) |
gdzie
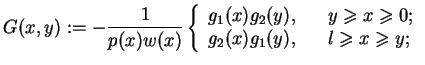 |
(13.8) |
nazywamy funkcją Green'a operatora 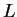 (13.1)
-(13.2).
(13.1)
-(13.2).
Funkcja Green'a ma takie własności:
- jest rzeczywista i ciągła w domkniętym kwadracie
![$ \overline{\sqcap}=[0,l] \times [0,l]$](img1556.gif) , jest klasy
, jest klasy
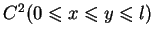 i
i
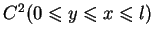 ;
;
- jest symetryczna:
- na przekątnej
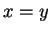 skok pochodnej
skok pochodnej
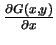 równa się
równa się
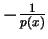 , tj.
, tj.
- przy
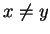 zachodzą równania jednorodne:
zachodzą równania jednorodne:
- są spełnione warunki brzegowe:
dla wszystkich
![$ y \in [0,l]$](img1566.gif) ;
;
-
Przykład. Funkcja Green'a problemu brzegowego
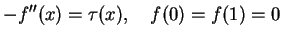 |
(13.9) |
ma wygląd
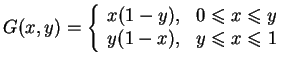 |
(13.10) |
Zastosujemy teraz wyrażenie (13.7) do problemu
spektralnego (13.1) i (13.2):
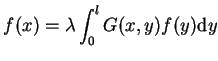 |
(13.11) |
gdzie
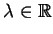 jest parametrem spektralnym.
Wyrażenie (13.11) ma tylko przeliczalną ilość
funkcji własnych
jest parametrem spektralnym.
Wyrażenie (13.11) ma tylko przeliczalną ilość
funkcji własnych
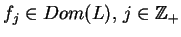 ,
przy
,
przy
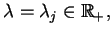
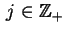 , tj.
, tj.
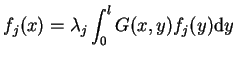 |
(13.12) |
gdzie zbiór
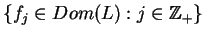 jest
gęsty w
jest
gęsty w
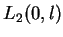 .
.
Przykład Niech
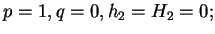 wtedy mamy taki problem spektralny:
wtedy mamy taki problem spektralny:
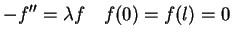 |
(13.13) |
Funkcje własne są
wartości własne są
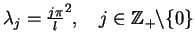 .
.



Next: Funkcje Bessel'a
Up: Problem Sturma-Liouville'a na
Previous: Problem Sturma-Liouville'a na
Andrzej Janus Szef
2001-12-05