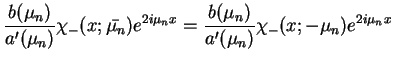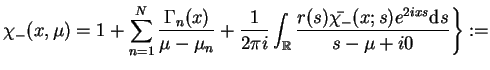Next: Schemat Gefllanda-Levitana- -Marczenki.
Up: Zagadnienie odwrotne problemu spektralnego
Previous: Problem spektralny dla operatora
Wyżej już ustaliliśmy, że widmo 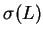 operatora
Schturm'a-Liouville'a (14.30) dla a priori zadanej
funkcji
operatora
Schturm'a-Liouville'a (14.30) dla a priori zadanej
funkcji
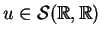 z warunkiem
(14.32) jest złożone ze skończonej ilości wartości
własnych
z warunkiem
(14.32) jest złożone ze skończonej ilości wartości
własnych
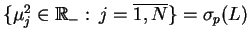 oraz jego ciągłej części
oraz jego ciągłej części
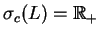 . Jest ciekawym i ważnym dla
zastosowań pytanie: czy jest wzajemniejednoznacznym odwzorowanie
. Jest ciekawym i ważnym dla
zastosowań pytanie: czy jest wzajemniejednoznacznym odwzorowanie
![$\displaystyle \mathcal{S}(\mathbb{R},\mathbb{R}) \ni u: \rightleftharpoons S[\sigma(L)]$](img1892.gif) |
(14.57) |
gdzie
![$ S[\sigma(L)]$](img1893.gif) jest zbiór tak zwanych ,,danych
spektralnych'', charakteryzujących problem spektralny
(14.31) w przestrzeni
jest zbiór tak zwanych ,,danych
spektralnych'', charakteryzujących problem spektralny
(14.31) w przestrzeni
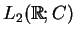 . To znaczy
że
. To znaczy
że
![$ S[\sigma(L)]= \sigma_{p} \cup \{a'(\mu_{j}) \neq 0: \,
j=\overline{1,N}\} \cu...
...ine{1,N}\}
\cup \{ b(\mu), a(\mu): {\mu}^2 \in \sigma_{c}(L)= \mathbb{R}_{+}\}$](img1894.gif) Zagadnienie odwrotne odwzorowania (14.57) daje
możliwość opisania zbioru tych potencjałów
Zagadnienie odwrotne odwzorowania (14.57) daje
możliwość opisania zbioru tych potencjałów
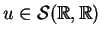 , które mają naprzód zadane dane
spektralne
, które mają naprzód zadane dane
spektralne
![$ S[\sigma(L)]$](img1893.gif) , zdefiniowane wyżej. Okazuje się że
zagadnienie odwroten może być rozwiązane w postaci jawnej i
dokładnie dla szerokiej klasy danych spektralnych
, zdefiniowane wyżej. Okazuje się że
zagadnienie odwroten może być rozwiązane w postaci jawnej i
dokładnie dla szerokiej klasy danych spektralnych
![$ S[\sigma(L)]$](img1893.gif) ,
co będzi naszym zadaniem poniżej.
,
co będzi naszym zadaniem poniżej.
W tym celu zdefiniujemy dwie nowe funkcje
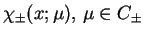 odpowiednie, gdzie
odpowiednie, gdzie
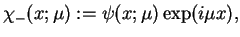 |
(14.58) |
Wykorzystując wyrażenia (14.40) i (14.43)
dość prosto wyprowadzić następujące równania, które
(14.58) spełniają na osi
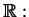
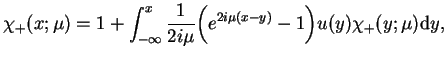 |
(14.59) |
dla
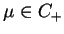 , i
dla
, i
dla
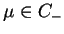 . Z wyrażeń (14.59) widać że
funkcja
. Z wyrażeń (14.59) widać że
funkcja
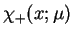 jest analityczna w
jest analityczna w 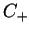 , a
, a
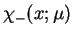 jest analityczna w
jest analityczna w 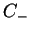 i zachodzą takie
wyrażenia asymptotyczne gdy
i zachodzą takie
wyrażenia asymptotyczne gdy
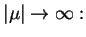
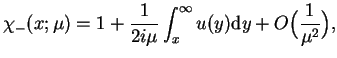 |
(14.60) |
Oprócz tego zauważmy tutaj jeszcze, że funkcja
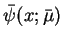 jest analityczna w
jest analityczna w 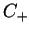 , co jest
skutkiem jej analityczności w
, co jest
skutkiem jej analityczności w 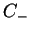 .
.
Mnożąc teraz (14.44) na
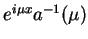 , na mocy definicji funkcji (14.58) znajdujemy:
, na mocy definicji funkcji (14.58) znajdujemy:
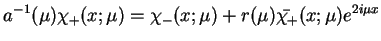 |
(14.61) |
gdzie
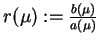 dla wszystkich
dla wszystkich
 Lewa strona (14.61) jest oczywiści
analitycznie przedłużalna w
Lewa strona (14.61) jest oczywiści
analitycznie przedłużalna w  , za wyjątkiem zer
, za wyjątkiem zer
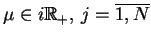 gdzie wyrażeie
gdzie wyrażeie
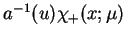 ma proste bieguny. Funkcja
ma proste bieguny. Funkcja
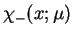 jest analityczna w
jest analityczna w 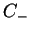 . To znaczy, że
można zdefiniować jedną funkcję
. To znaczy, że
można zdefiniować jedną funkcję
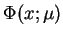 na całej
płaszczyźnie
na całej
płaszczyźnie 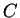 , takiej że
, takiej że
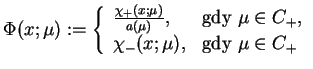 |
(14.62) |
i mającej skok na osi rzeczywistej
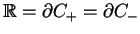 w takiej postaci:
w takiej postaci:
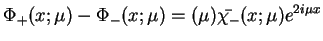 |
(14.63) |
dla wszystkich
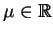 , gdzie
, gdzie
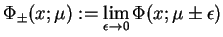 |
(14.64) |
Na mocy (14.47) i (14.60) stwierdzamy że
funkcja
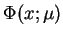 spełnia przy
spełnia przy
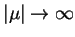 taki
asymptotyczny warunek:
taki
asymptotyczny warunek:
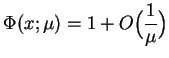 |
(14.65) |
To znaczy że funkcja
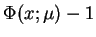 rozpatrywana na
rozpatrywana na
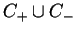 spełnia warunek Cauchy'ego:
spełnia warunek Cauchy'ego:
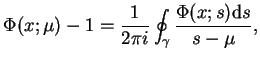 |
(14.66) |
gdzie kawałkami gładki kontur
 ma wygląd jak na rysunku:
ma wygląd jak na rysunku:
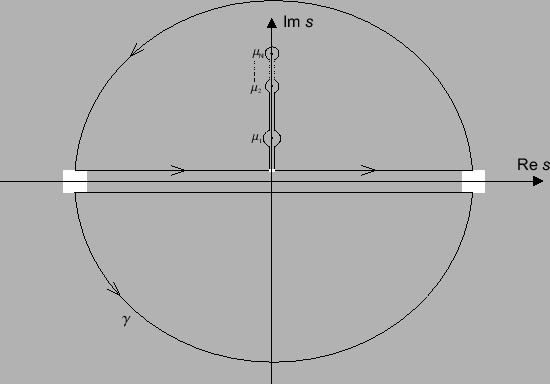
Rys. 10
|
Wyliczając całkę po prawej stronie (14.66),
znajdujemy że
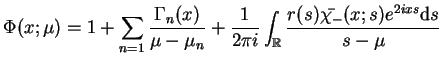 |
(14.67) |
gdzie
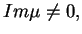 tj,
tj,
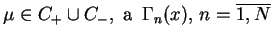 są reszty, które mogą być
powiązane z wartościami funkcji
są reszty, które mogą być
powiązane z wartościami funkcji
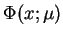 w punktach
w punktach
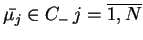 , tj. z
wartościami
, tj. z
wartościami
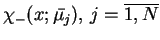 .
Mianowicie, z (14.67),(14.62) i
(14.61) otrzymujemy, że
.
Mianowicie, z (14.67),(14.62) i
(14.61) otrzymujemy, że
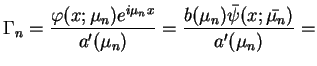 |
(14.68) |
dla wszystkich
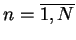 . Tak więc mamy z
(14.69):
. Tak więc mamy z
(14.69):
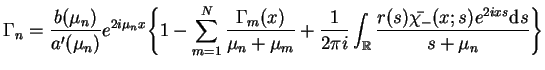 |
(14.69) |
gdzie
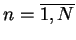 . Niech teraz
. Niech teraz
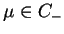 w wyrażeniu
(14.67) dąży z dołu do osi rzeczywistej
w wyrażeniu
(14.67) dąży z dołu do osi rzeczywistej
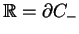 . Wtedy oczywiście na mocy
(14.62) znajdziemy:
. Wtedy oczywiście na mocy
(14.62) znajdziemy:
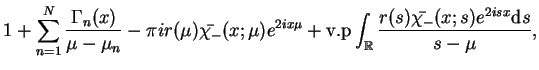 |
(14.70) |
gdzie
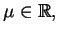 oraz całka v.p
oraz całka v.p
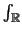 znaczy wzięcie niewłaściwej całki w sensie wartości
głównej. Teraz można wykorzystać wyrażenie (14.60)
dla znalezienia funkcji potencjału
znaczy wzięcie niewłaściwej całki w sensie wartości
głównej. Teraz można wykorzystać wyrażenie (14.60)
dla znalezienia funkcji potencjału
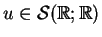 przez (14.70):
przez (14.70):
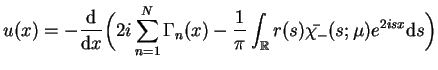 |
(14.71) |
Jako równania całkowe wyrażenia (14.69) i
(14.70) są jednoznacznie rozwiązalne. Współczynnik
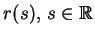 , w (14.71) ma spełniać
zgodnie z (14.61) takie warunki:
, w (14.71) ma spełniać
zgodnie z (14.61) takie warunki:
- i)
-
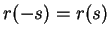 ;
;
- ii)
-
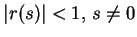 ;
;
- iii)
-
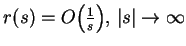 ;
;
- iv)
-
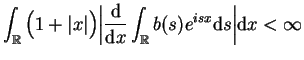 |
(14.72) |
gdzie ostatni warunek  gwarantuje że potencjał
gwarantuje że potencjał
 znaleziony wg. wzoru (14.71)
będzie sprawdzać warunek (14.32)
znaleziony wg. wzoru (14.71)
będzie sprawdzać warunek (14.32)



Next: Schemat Gefllanda-Levitana- -Marczenki.
Up: Zagadnienie odwrotne problemu spektralnego
Previous: Problem spektralny dla operatora
Andrzej Janus Szef
2001-12-05
![]() odpowiednie, gdzie
odpowiednie, gdzie
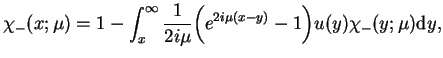
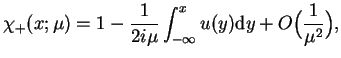
![]() , na mocy definicji funkcji (14.58) znajdujemy:
, na mocy definicji funkcji (14.58) znajdujemy: