Przykład 5.1
Czytelnik który rozwiązał ćwiczenie
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
stwierdził z pewnością,
że z pierwszego słownika
|
(5.7) |
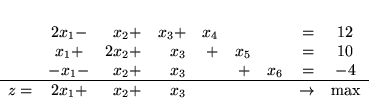 |
w którym rozwiązanie bazowe
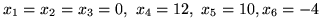
nie jest rozwiązaniem dopuszczalnym, otrzymał słownik
w którym rozwiązanie bazowe jest dopuszczalne, mianowicie
|
(5.8) |
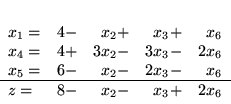 |
Zmiennymi bazowymi słownika (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
) są
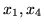
i
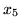
.
Macierzowo słownik (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
) można zapisać następująco
|
(5.9) |
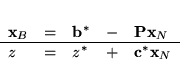 |
gdzie
![${\bf P} = \left[
\begin{array}{rrr}
1 & -1 & -1 \\
-3 & 3 & 2 \\
1 & 2 & ...
...rray}{c}
4\\
4\\
6
\end{array}
\right], \ z^*=8, \ {\bf c}^* = [-1,-1,2]$](img499.gif)
, zaś
![${\bf x}_N = \left[
\begin{array}{c}
x_2\\
x_3\\
x_6
\end{array}
\right] $](img500.gif)
Przykład 5.1 (c.d.)
Dla zmiennych bazowych
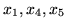
mamy:
Ponieważ w naszym przykładzie macierz
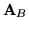
jest nieosobliwa,
możemy z równania (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
) obliczyć
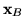
|
(5.11) |
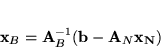 |
Przykład 5.1 (dokończenie)
W ostatnim słowniku naszego przykładu jedynym współczynnikiem dodatnim funkcji
celu jest współczynnik przy
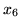
. Zmienną wchodzącą będzie więc
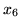
.
Równie łatwo zauważyć, że zmienną wychodzącą jest
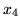
.
W nowym słowniku zmiennymi bazowymi będą więc
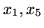
i
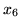
,
zmiennymi niebazowymi
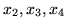
. Wobec tego macierzą bazową
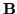
jest macierz złożona z pierwszej, piątej i szóstej kolumny macierzy
czyli
![${\bf c}_B=[2,0,0]$](img545.gif)
,
![${\bf c}_N=[1,1,0]$](img546.gif)
.
Obliczmy najpierw wektor
z równania
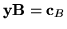
Stąd oczywiście zmienną wchodzącą jest koniecznie
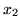
(jedyną dodatnią współrzędną wektora
![$[2,0,-1]$](img554.gif)
jest
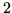
,
współrzędna odpowiadająca zmiennej
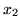
).
Źeby wyznaczyć zmienną wychodzącą, musimy w pierwszym równaniu
(
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
) wyznaczyć wektor
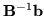
i
pierwszą kolumnę
(tę odpowiadającą zmiennej
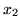
) macierzy
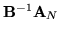
.
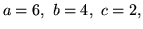
a więc
Z kolei pierwszą kolumną
![$\left[ \begin{array}{c} k_1 \\ k_2 \\ k_3 \end{array}
\right]$](img560.gif)
macierzy
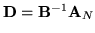
wyznaczymy z równania
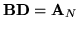
, a więc
(po lewej stronie tej równości jest iloczyn macierzy
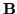
przez pierwszą kolumnę macierzy
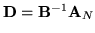
,
z prawej pierwsza kolumna
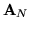
).
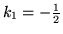
,
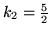
,
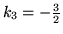
.
Pomijając nieistotne dla nas zmienne niebazowe
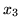
i
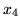
równanie
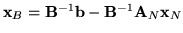
słownika
(
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
) oznacza w w naszym przypadku
Jedynym współczynnikiem ujemnym przy
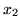
jest
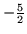
i zmienną wychodząca jest
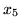
.
Tak więc nowymi zmiennmi bazowymi są
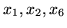 , a zmiennymi niebazowymi
, a zmiennymi niebazowymi
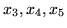 . Nowe macierze i wektory
. Nowe macierze i wektory
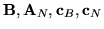 to teraz
to teraz
-
![${\bf B} = \left[ \begin{array}{rrr}
2 & -1 & 0 \\
1 & 2 & 0\\
-1 & -1 & 1
...
...& 1 \\
1 & 0 & 0
\end{array} \right], {\bf c}_B=[2,1,0], {\bf c}_N=[1,0,0]. $](img573.gif)
Znowu liczymy
![${\bf y}=[y_1,y_2,y_3]$](img574.gif)
z równania
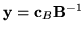
, czyli
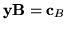
.
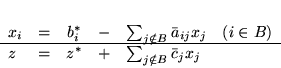
![\begin{displaymath}{\bf A}^*=\left[
\begin{array}{ccccccc}
a_{11} & ... & a_{1...
...ay}{c} \
b_1 \\
.\\
.\\
.\\
b_m
\end{array}
\right],\end{displaymath}](img489.gif)
![\begin{displaymath}{\bf c}=[c_1,...,c_n],
{\bf x}=\left[\begin{array}{l}
x_1\...
...array}{c}
x_1\\
.\\
.\\
.\\
x_n
\end{array}
\right] \end{displaymath}](img490.gif)
![\begin{displaymath}{\bf x}_B = \left[
\begin{array}{l}
x_{n+1}\\
.\\
.\\
.\\
x_{n+m}
\end{array}
\right]
\end{displaymath}](img493.gif)
![${\bf P} = \left[
\begin{array}{rrr}
1 & -1 & -1 \\
-3 & 3 & 2 \\
1 & 2 & ...
...rray}{c}
4\\
4\\
6
\end{array}
\right], \ z^*=8, \ {\bf c}^* = [-1,-1,2]$](img499.gif) , zaś
, zaś
![${\bf x}_N = \left[
\begin{array}{c}
x_2\\
x_3\\
x_6
\end{array}
\right] $](img500.gif)
![\begin{displaymath}{\bf A}_B = \left[
\begin{array}{ccc}
2 & 1 & 0 \\
1 & 0 ...
...[
\begin{array}{c}
x_2\\
x_3\\
x_6
\end{array}
\right] \end{displaymath}](img507.gif)
![\begin{displaymath}{\bf A}= \left[
\begin{array}{rrrrrr}
2 & -1 & 1 & 1 & 0 & ...
... 0 & 1 & 0 \\
-1 & -1 & 1 & 0 & 0 & 1
\end{array}
\right]
\end{displaymath}](img543.gif)
![\begin{displaymath}
{\bf B}=\left[
\begin{array}{rrr}
2 & 0 & 0\\
1 & 1 & 0...
... & 1 & 1 \\
2 & 1 & 0 \\
-1 & 1 & 0
\end{array}
\right]
\end{displaymath}](img544.gif)
![\begin{displaymath}[y_1,y_2,y_3]\left[
\begin{array}{rrr}
2 & 0 & 0\\
1 & 1 & 0\\
-1 & 0 & 1
\end{array}
\right] = [2,0,0] \end{displaymath}](img549.gif)
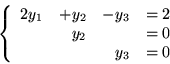
![\begin{displaymath}{\bf c}_B{\bf B}^{-1}{\bf A}_N = [1,0,0]
\left[
\begin{arra...
...\\
2 & 1 & 0 \\
-1 & 1 & 0
\end{array} \right] = [-1,1,1] \end{displaymath}](img552.gif)
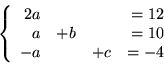
![\begin{displaymath}
{\bf B}^{-1}{\bf b} = \left[
\begin{array}{c}
6\\
4\\
2
\end{array} \right] \end{displaymath}](img559.gif)
![$\left[ \begin{array}{c} k_1 \\ k_2 \\ k_3 \end{array}
\right]$](img560.gif) macierzy
macierzy
![\begin{displaymath}
\left[
\begin{array}{rrr}
2 & 0 & 0 \\
1 & 1 & 0 \\
-...
...left[ \begin{array}{r}
-1 \\
2 \\
-1
\end{array} \right] \end{displaymath}](img563.gif)
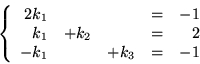
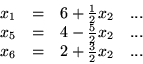
![${\bf B} = \left[ \begin{array}{rrr}
2 & -1 & 0 \\
1 & 2 & 0\\
-1 & -1 & 1
...
...& 1 \\
1 & 0 & 0
\end{array} \right], {\bf c}_B=[2,1,0], {\bf c}_N=[1,0,0]. $](img573.gif)
![\begin{displaymath}[y_1,y_2,y_3]\left[\begin{array}{rrr}2 & -1 & 0 \\ 1 & 2 & 0 \\ -1 & -1 & 1
\end{array}\right] = [2,1,0] \end{displaymath}](img577.gif)
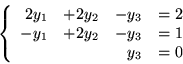
![${\bf c}_B{\bf B}^{-1}{\bf A}_N = {\bf y}{\bf A}_N =
[\frac{3}{5},\frac{4}{5},...
...0 & 1 \\ 1 & 0 & 0\end{array}\right] =
[\frac{7}{5}, \frac{3}{5},\frac{4}{5}]$](img581.gif)
![\begin{displaymath}\left[
\begin{array}{c}x_1\\ x_2\\ x_6 \end{array} \right]
= {\bf B}^{-1}{\bf b} \end{displaymath}](img584.gif)
![$z=z^*+{\bf c}_B{\bf B}^{-1}{\bf b}=0+[\frac{3}{5},\frac{4}{5},0]
\left[ \begin...
...2\\ 10 \\ -4 \end{array} \right]
= \frac{36}{5} + \frac{40}{5} = \frac{76}{5}$](img586.gif) .
.