




Next: Programowanie całkowite
Up: Zredukowana metoda sympleksowa
Previous: Macierzowy opis słownika
Spis rzeczy
Indeks
W zrewidowanej metodzie sympleksowej oszczędzamy -
w porównaniu z metodąoryginalną
przedstawioną w rozdziale trzecim - czas i pamięć (komputera).
- Czas
- - bowiem nie liczymy iloczynu
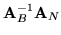 a tylko jego jedną kolumnę.
To w praktycznych zadaniach PL bardzo istotna oszczędność,
bowiem na ogół zmiennych,
a więc kolumn macierzy jest bardzo dużo.
a tylko jego jedną kolumnę.
To w praktycznych zadaniach PL bardzo istotna oszczędność,
bowiem na ogół zmiennych,
a więc kolumn macierzy jest bardzo dużo.
- Pamięć
- - ponieważ do kolejnych obliczeń w ogóle nie są nam
potrzebne żadne słowniki poprzednie, poza słownikiem pierwszym.
Każdą iterację w metodzie zredukowanej można opisać następująco:
- Krok 1.
- Obliczamy
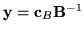 (z równania
(z równania
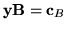 )5.2
)5.2
- Krok 2.
- Jeśli
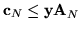 to aktualna rozwiązaniebazowe
jest optymalne.
Jeśli nie, to znaczy dla pewnej kolumny
to aktualna rozwiązaniebazowe
jest optymalne.
Jeśli nie, to znaczy dla pewnej kolumny 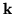 macierzy
macierzy 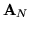 zachodzi
zachodzi
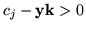 ,
dla odpowiedniejwspółrzędnej
,
dla odpowiedniejwspółrzędnej 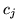 wektora
wektora 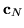 , to kolumna
, to kolumna 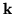 wyznacza zmienną wychodzącą.
wyznacza zmienną wychodzącą.
- Krok 3.
- Obliczamy kolumnę
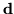 macierzy
macierzy
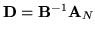 ,
odpowiadającą zmiennej wchodzącej.
Jeśli wszystkie jej współrzędne są ujemne, to problem jest nieograniczony.
W przeciwnym przypadku jako zmienną wychodzącą wybieramy tę dla której iloraz
,
odpowiadającą zmiennej wchodzącej.
Jeśli wszystkie jej współrzędne są ujemne, to problem jest nieograniczony.
W przeciwnym przypadku jako zmienną wychodzącą wybieramy tę dla której iloraz
jest minimalny (i nieujemny).
- Krok 4.
- Ustalamy nowe zmienne bazowe i niebazowe i
dla nich wartości dla macierzy
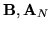 oraz wektorów
oraz wektorów 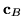 i
i 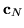 .
.





Next: Programowanie całkowite
Up: Zredukowana metoda sympleksowa
Previous: Macierzowy opis słownika
Spis rzeczy
Indeks