




Next: Ćwiczenia
Up: Zredukowana metoda sympleksowa
Previous: Podsumowanie
Spis rzeczy
Indeks
Programowanie liniowe
w liczbach całkowitych
Bardzo często w zadaniach praktycznych jest tak, że jedynymi interesującymi
rozwiązaniami
problemów programowania matematycznego w ogólności,
a liniowego w szczególności, są
rozwiązania całkowite.
Dla przykładu, jeśli 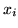 są zmiennymi decyzyjnymi,
a więc mogącymi przyjmowaćtości
są zmiennymi decyzyjnymi,
a więc mogącymi przyjmowaćtości
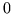 lub
lub 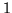 , to najczęściej rozwiązania niecałkowite
nie mają żadnej sensownej interpretacji.
, to najczęściej rozwiązania niecałkowite
nie mają żadnej sensownej interpretacji.
Przykład 5.2
W pewnym przedsiębiorstwie
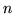
osób ma wykonywać
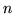
czynności, przy czym:
- -
- każda osoba ma wykonywać jedną (i tylko jedną) czynność,
- -
- koszt przystosowania
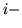 tej osoby do wykonywania
tej osoby do wykonywania
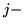 ej czynności wynosi
ej czynności wynosi 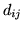 .
.
Zadanie polega na przyporządkowaniu każdej z osób zadania w taki
sposób, by suma kosztów
była możliwie najmniejsza.
Połóżmy
Problem programowania liniowego jaki otrzymamy dla tego zadania
jest następujący.
Problem przydziału:
Okazuje się, że zadanie programowania liniowego w liczbach
całkowitych jest problemem
trudnym, któremu jest poświęcona bardzo obszerna literatura. Zainteresowanego
czytelnika odsyłam do rozdziału osiemnastego [19], w którym poza wielu
innymi rezultatami znajdzie twierdzenie mówiące, że jeśli
współczynniki macierzy 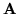 i wektora
i wektora 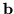 są wymierne, to problem
są wymierne, to problem
jest 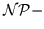 zupełny.
Ogólna postać programowania liniowego w liczbach całkowitych jest następująca:
zupełny.
Ogólna postać programowania liniowego w liczbach całkowitych jest następująca:
|
(5.14) |
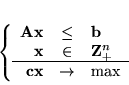 |
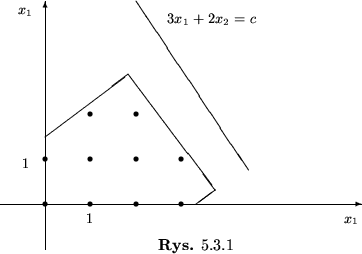
Przykład 5.3
Rozważmy PPL
|
(5.15) |
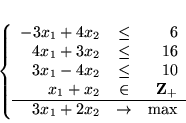 |
Na rysunku 5.3.1 przedstawiono interpretację geometryczną zadania (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
).
Łatwo zauważyć, że rozwiązaniem optymalnym problemu
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
)
jest
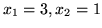
, a więc punkt znajdujący sie wewnątrz zbioru rozwiązań
dopuszczalnych problemu powstałego z (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
) przez usunięcie
założeń o całkowitości zmiennych. Taki punkt jest oczywiście nie do
wykrycia przez algorylm sympleks.

W dalszym ciągu zajmiemy się sytuacją w której problem programowania
liniowego w liczbach całkowitych ma rozwiązanie które można otrzymać
stosując metodę sympleks. W rozdziale ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) okaże się, że z takimi
właśnie sytuacjami mamy do czynienia częściej niż mogłoby się, na
pierwszy rzut oka, wydawać.
okaże się, że z takimi
właśnie sytuacjami mamy do czynienia częściej niż mogłoby się, na
pierwszy rzut oka, wydawać.
Definicja 5.2
Mówimy, że macierz
jest
totalnie unimodularna,
jeżeli dla każdej podmacierzy kwadratowej
macierzy
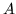
zachodzi
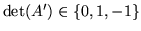
.
Przykład 5.4
Z łatwością można sprawdzić, że macierz
jest totalnie unimodularna.
Z definicji macierzy unimodularnych wynika natychmiast, że jej współrzędne są równe
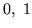 lub
lub 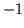 .
.
Udowodnimy następujące twierdzenie.
Twierdzenie 5.2
Niech będzie dany PPL
|
(5.16) |
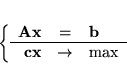 |
gdzie
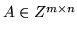
jest macierzą rzędu
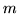
i
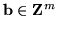
.
Jeśli dla każdej macierzy bazowej
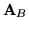
zachodzi
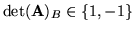
, to
-
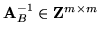 ,
,
- każde rozwiązanie bazowe
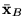 jest całkowite.
jest całkowite.
Dowód. W podrozdziale ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) widzieliśmy,
że ograniczenia w problemie (
widzieliśmy,
że ograniczenia w problemie (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) )
można zapisać w postaci
)
można zapisać w postaci
|
(5.17) |
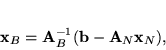 |
gdzie 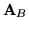 i
i 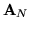 są pewnymi podmacierzami
macierzy
są pewnymi podmacierzami
macierzy 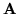 , zaś
, zaś 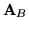 jest nieosobliwą macierzą kwadratową rzędu
jest nieosobliwą macierzą kwadratową rzędu 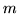 .
Jeśli oznaczymy wyrazy macierzy
.
Jeśli oznaczymy wyrazy macierzy
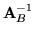 przez
przez
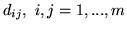 , to
, to
gdzie
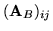 jest macierzą powstałą z
jest macierzą powstałą z 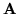 przez skreślenie
przez skreślenie 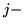 tego wiersza
i
tego wiersza
i 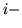 tej kolumny. Jest więc zupełnie oczywiste, że
tej kolumny. Jest więc zupełnie oczywiste, że
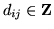 dla wszystkich
dla wszystkich
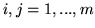 . W rozwiązaniu bazowym
. W rozwiązaniu bazowym 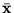 mamy
mamy
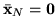 i
i
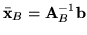 (por. (
(por. (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) )). Ponieważ
)). Ponieważ 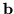 jest
z założenia wektorem o współczynnikach całkowitych, także wektor
jest
z założenia wektorem o współczynnikach całkowitych, także wektor 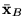 ma współczynniki całkowite.
Twierdzenie
ma współczynniki całkowite.
Twierdzenie ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) pociąga natychmiast podany niżej ważny wniosek który
ostatecznie wyjaśnia rolę macierzy totalnie unimodularnych w
całkowitoliczbowym programowaniu liniowym.
pociąga natychmiast podany niżej ważny wniosek który
ostatecznie wyjaśnia rolę macierzy totalnie unimodularnych w
całkowitoliczbowym programowaniu liniowym.
Wniosek 5.3
Niech będzie dany PPL
|
(5.18) |
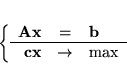 |
gdzie
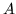
jest pewną macierzą totalnie unimodularną, zaś
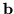
wektorem
o współczynnikach całkowitych.
- Jeżeli (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) jest niesprzeczny, to jego rozwiązania bazowe mają
wszystkie współrzędne całkowite.
) jest niesprzeczny, to jego rozwiązania bazowe mają
wszystkie współrzędne całkowite.
- Jeżeli istnieje rozwiązania optymalne problemu (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ), to istnieją
takie rozwiązania optymalne których wszystkie współrzędne są całkowite.
), to istnieją
takie rozwiązania optymalne których wszystkie współrzędne są całkowite.
- Jeśli problem (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) jest niesprzeczny i ograniczony to algorytm
sympleks znajduje takie rozwiązanie (
) jest niesprzeczny i ograniczony to algorytm
sympleks znajduje takie rozwiązanie (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) którego wszystkie
współrzędne są liczbami całkowitymi.
) którego wszystkie
współrzędne są liczbami całkowitymi.
Wobec wniosku ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ważnym jest problem ozpoznania" macierzy totalnie
unimodularnych. W rozdziale
ważnym jest problem ozpoznania" macierzy totalnie
unimodularnych. W rozdziale ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) okaże się jak ważnym warunkiem wystarczającym
dla tych macierzy jest poniższe twierdzenie.
okaże się jak ważnym warunkiem wystarczającym
dla tych macierzy jest poniższe twierdzenie.
Przykład 5.5
Macierz
(podobnie jak macierz z przykładu
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
) spełnia założenia twierdzenia
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
,
w więc jest macierzą totalnie unimodularną.
Dowód twierdzenia ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) . Wystarczy wykazać, że dla każdej macierzy
. Wystarczy wykazać, że dla każdej macierzy
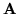 o
o 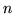 wierszach i
wierszach i 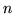 kolumnach spełniającej założenia twierdzenia
kolumnach spełniającej założenia twierdzenia
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
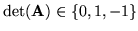 . Dowód przeprowadzimy przez indukcję
ze względu na
. Dowód przeprowadzimy przez indukcję
ze względu na 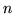 .
.
Dla 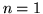 przwdziwość twierdzenia jest oczywista. Przypuśćmy, więc, że
przwdziwość twierdzenia jest oczywista. Przypuśćmy, więc, że 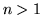 i twierdzenie jest prawdziwe dla macierzy o
i twierdzenie jest prawdziwe dla macierzy o 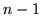 wierszach i
wierszach i 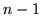 kolumnach.
Rozpatrzymy trzy przypadki:
kolumnach.
Rozpatrzymy trzy przypadki:
- Przypadek 1.
- Jedna z kolumn macierzy
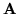 ma wszystkie wyrazy równe
ma wszystkie wyrazy równe 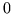 . Wtedy
oczywiście
. Wtedy
oczywiście
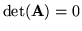 .
.
- Przypadek 2.
- W jednej z kolumn jest jeden wyraz różny od zera, powiedzmy że tym wyrazem jest
 . Wtedy
. Wtedy
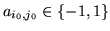 .
Rozwijamy wyznacznik macierzy
.
Rozwijamy wyznacznik macierzy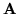 względem kolumny
względem kolumny 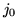 i otrzymujemy
i otrzymujemy
|
(5.19) |
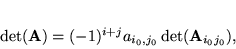 |
gdzie
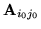 jest macierzą powstałą przez skreślenie w
jest macierzą powstałą przez skreślenie w 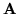 wiersza
wiersza 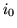
i kolumny 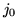 .
Zauważmy, że macierz
.
Zauważmy, że macierz
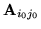 jest macierzą kwadratową o
jest macierzą kwadratową o 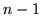 wierszach i kolumnach spełniającą warunki twierdzenia
wierszach i kolumnach spełniającą warunki twierdzenia ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) i wobec tego
i wobec tego
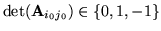 . Stąd i (
. Stąd i (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) otrzymujemy
) otrzymujemy
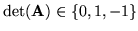 .
.
- Przypadek 3.
- Nie zachodzą przypadki 1 ani 2. Wtedy
|
(5.20) |
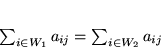 |
dla każdego 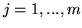 . Udowodnienie, że w tym przypadku
. Udowodnienie, że w tym przypadku
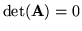 jest bardzo prostym
ćwiczeniem, które pozostawiam czytelnikowi (p. ćwiczenie
jest bardzo prostym
ćwiczeniem, które pozostawiam czytelnikowi (p. ćwiczenie ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ).
).





Next: Ćwiczenia
Up: Zredukowana metoda sympleksowa
Previous: Podsumowanie
Spis rzeczy
Indeks
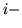 tej osoby do wykonywania
tej osoby do wykonywania
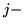 ej czynności wynosi
ej czynności wynosi 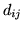 .
.
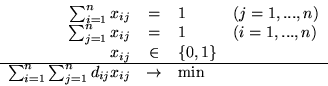
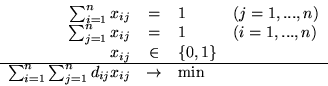
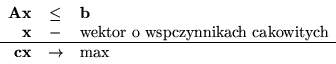
![\begin{displaymath}{\bf B} = \left[ \begin{array}{cccccc}
1&0&-1&-1&0&0\\
0&1...
...
\end{array}\right]\begin{array}{c}W_1\\ W_1\\ W_1\end{array},\end{displaymath}](img632.gif)