




Next: Ćwiczenia
Up: Zadanie ograniczone
Previous: Sympleks dla zadania ograniczonego
Spis rzeczy
Indeks
Podobnie jak w przypadku standardowego PPL także w przypadku zadania
ograniczonego istnieje
problem inicjalizacji, to znaczy znalezienia jakiegokolwiek bazowego rozwiązania
dopuszczalnego czyli pierwszego dopuszczalnego słownika. Także w tym przypadku
w poszukiwanie takiego słownika wprzęgniemy metodę sympleks.
Z zadaniem
|
(6.6) |
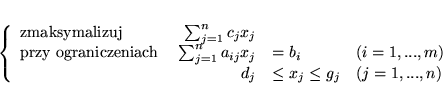 |
skojarzymy zadanie PL w którym ograniczenia będą postaci:
|
(6.7) |
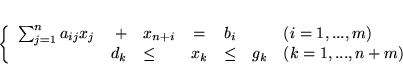 |
przy czym dla 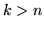 dolne i górne ograniczenia we wzorze (
dolne i górne ograniczenia we wzorze (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) są
wyznaczane w sposób
opisany poniżej.
) są
wyznaczane w sposób
opisany poniżej.
Niech
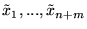 będą dane następującymu wzorami:
będą dane następującymu wzorami:
Jeśli
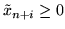 to w (
to w (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) przyjmujemy
) przyjmujemy
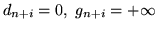 , jeśli zaś
, jeśli zaś
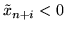 to
to
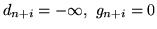 .
.
Jest oczywiste, że (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) ma rozwiązanie dopuszczalne wtedy
i tylko wtedy, gdy (
) ma rozwiązanie dopuszczalne wtedy
i tylko wtedy, gdy (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) ma rozwiązanie w którym
) ma rozwiązanie w którym
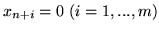 .
Problemem ograniczonym PL który wystarczy rozwiązać jest
.
Problemem ograniczonym PL który wystarczy rozwiązać jest
|
(6.8) |
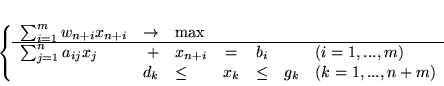 |
gdzie
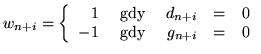 .
Problem (
.
Problem (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) jest niesprzeczny,
) jest niesprzeczny,
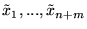 jest jego rozwiązaniem
dopuszczalnym.
Jeśli (
jest jego rozwiązaniem
dopuszczalnym.
Jeśli (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) ma rozwiązanie optymalne zerowe (
) ma rozwiązanie optymalne zerowe (
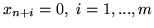 ), to pierwszych
), to pierwszych
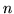 współrzędnych tego rozwiązania
współrzędnych tego rozwiązania
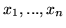 jest rozwiązaniem dopuszczalnym
(
jest rozwiązaniem dopuszczalnym
(![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ).
).
Subsections





Next: Ćwiczenia
Up: Zadanie ograniczone
Previous: Sympleks dla zadania ograniczonego
Spis rzeczy
Indeks
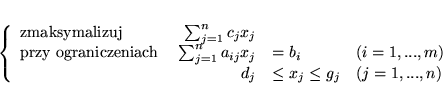
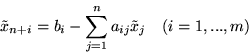
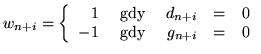 .
Problem (
.
Problem (