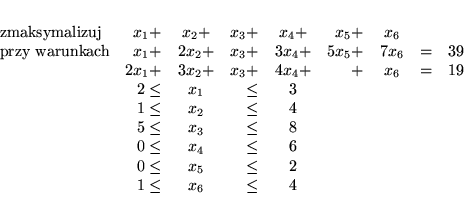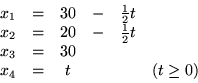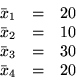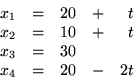Przykład 6.2
Przyjmijmy jako zmienne bazowe
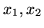
i weźmy
rozwiązanie bazowe
Wartość funkcji celu dla naszego rozwiązania bazowego wynosi
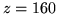
.
Będziemy, tak jak w metodzie sympleks, zmieniać wartości jednej ze zmiennych
niebazowych tak, aby powiększała się wartość rozwiązania, przy zachowaniu
warunków ograniczających, a w szczególności pierwszych dwóch równań
warunków ograniczających.
Wybierzmy zmienną
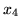
jako tę zmienną niebazową niebazową której
powiększenie powoduje zwiększanie funkcji celu.
Zauważmy, że jeżeli podstawimy
to także takie zmienne spełniają oba równania w
ograniczeniach naszego zdania PL.
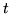
możemy
zwiększyć do 20. Wtedy otrzymamy
Przyjąć więc można:
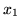
oraz
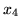
jako zmienne bazowe oraz
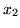
i
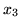
jako zmienne niebazowe. Nowe rozwiązanie ma wartość
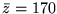
.
Teraz zmienną wchodzącą będzie
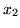
.
Podobnie jak poprzednio zauważmy, że podstawiając
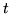
możemy zwiększyć do
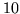
(rozpoczynając od
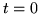
),
wtedy jednak funkcja celu maleje - a więc naszego rozwiązania nie da się już poprawić.
Obserwacja 6.1
Jeżeli w rozwiązaniu bazowym
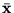
zastąpimy
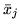
przez
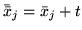
,
a pozostałe współrzędne niebazowe wektora
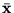
nie ulegną zmianie, to
gdzie
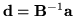
,
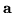
jest
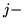
tą kolumną
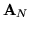
oraz
Twierdzenie 6.2
Jeśli metoda sympleks dla problemu ograniczonego (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
) nie
doprowadza do rozwiązania
w skończonej liczbie kroków, to algorytm wpada w pętlę.
Twierdzenie 6.3
Jeśli do wyboru zmiennych wchodzących i wychodzących w algorytmie sympleks dla
problemu ograniczonego (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
) stosujemy regułę Blanda, to algorytm kończy się po
skończonej liczbie iteracji.
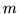 zmiennych bazowych oraz
zmiennych bazowych oraz
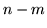 zmiennych niebazowych
zmiennych niebazowych
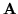 których elementy są współczynnikami
przy zmiennych bazowych tworzą macierz (kwadratową o
których elementy są współczynnikami
przy zmiennych bazowych tworzą macierz (kwadratową o 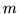 wierszach i
wierszach i 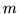 kolumnach)
nieosobliwą,
kolumnach)
nieosobliwą,
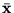 równe są ich
ograniczeniom górnym lub dolnym.
równe są ich
ograniczeniom górnym lub dolnym.