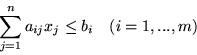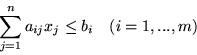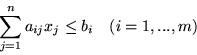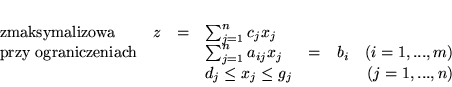Next: Sympleks dla zadania ograniczonego
Up: Wykłady z programowania liniowego
Previous: Ćwiczenia
Spis rzeczy
Indeks
W wielu praktycznych zagadnieniach obok ograniczeń
występują indywidualne ograniczenia od góry na zmienne (wszystkie lub niektóre postaci
Zadanie PL z tak określonymi ograniczeniami jest wtedy oczywiście zadaniem
w postaci standardowej
Jednak po dołączeniu zmiennych sztucznych otrzymujemy wtedy macierz
ograniczeń o rozmiarze
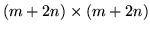 . Jeśli liczba zmiennych (a więc liczba
. Jeśli liczba zmiennych (a więc liczba 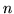 ) jest duża,
wielkość problemu który należało będzie rozwiązać może być kłopotliwa.
Stąd istotna może się okazać metoda zasugerowana po raz pierwszy przez Dantziga
w [5].
) jest duża,
wielkość problemu który należało będzie rozwiązać może być kłopotliwa.
Stąd istotna może się okazać metoda zasugerowana po raz pierwszy przez Dantziga
w [5].
Problem postawimy jeszcze ogólniej niż wspomniano wyżej, mianowicie będziemy
zakładać ograniczenia nie tylko górne ale i dolne i to na wszystkie zmienne, czyli
przy czym dopuszczać będziemy 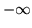 dla dolnego i
dla dolnego i 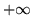 dla górnego ograniczenia
(co oczywiście oznacza, że odpowiednich ograniczeń nie ma)
6.1
Będziemy też zakładali równości
dla górnego ograniczenia
(co oczywiście oznacza, że odpowiednich ograniczeń nie ma)
6.1
Będziemy też zakładali równości
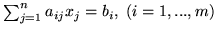 , czyli sytuację
którą mamy po wprowadzeniu zmiennych sztucznych. Problem nasz będzie więc postaci
, czyli sytuację
którą mamy po wprowadzeniu zmiennych sztucznych. Problem nasz będzie więc postaci
lub w formie macierzowej
|
(6.1) |
 |
gdzie
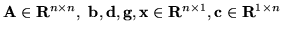 .
.
Subsections





Next: Sympleks dla zadania ograniczonego
Up: Wykłady z programowania liniowego
Previous: Ćwiczenia
Spis rzeczy
Indeks