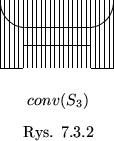Next: Układy nierówności i równań
Up: Interpretacje i zastosowania
Previous: Komentarz
Spis rzeczy
Indeks
Powłoki wypukłe zbiorów
Definicja 7.1
Mówimy, że podzbiór
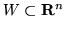
jest
wypukły
7.3 jeżeli dla każdych dwóch elementów
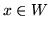
i
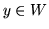
odcinek je łączący:
jest zawarty w
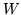
.
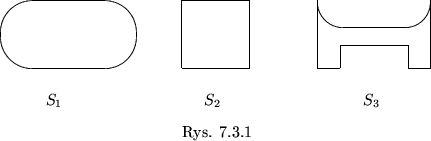
Przykład 7.3
Jest oczywistym, że jedynymi podzbiorami wypukłymi
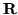
sa przedziały.
W
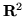
zbiory
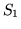
i
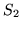
przedstawione na rysunku 7.3.1 są wypukłe,
zaś
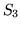
nie jest zbiorem wypukłym.
Banalnie prosty do udowodnienia jest następujący wniosek którego dowód
wobec tego pozostawiamy czytelnikowi.
Wniosek 7.1
Niech
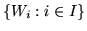
będzie rodziną zbiorów wypukłych. Wtedy przecięcie
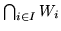
jest także zbiorem wypukłym.

Wniosek ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) , jakkolwiek by nie był prosty do udowodnienia jest odpowiedzialny
za bardzo ważne pojęcie powłoki wypukłej zbioru.
, jakkolwiek by nie był prosty do udowodnienia jest odpowiedzialny
za bardzo ważne pojęcie powłoki wypukłej zbioru.
Definicja 7.2
Niech
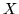
będzie dowolnym podzbiorem
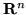
.
Powłoką wypukłą 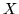
nazywamy najmniejszy
(w sensie zawierania zbiorów) zbiór wypukły
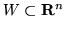
zawierający
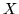
. Piszemy wtedy
Przykład 7.4
Dla zbioru
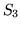
z rysunku 7.3.1 powłoka wypukła przedstawiona jest na rysunku 7.3.2.
Wniosek 7.2
Niech
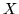
będzie dowolnym zbiorem zawartym w
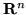
i niech
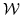
będzie
rodziną wszystkich zbiorów wypukłych zawierających
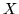
. Wtedy
Dowód. Ponieważ
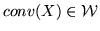
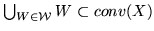 .
Z drugiej strony, skoro
.
Z drugiej strony, skoro 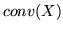 jest najmniejszym, w sensie zawierania zbiorów, zbiorem
wypukłym zawierającym
jest najmniejszym, w sensie zawierania zbiorów, zbiorem
wypukłym zawierającym 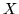 , zachodzi
, zachodzi
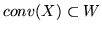 dla każdego
dla każdego
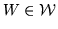 . Stąd zaś
. Stąd zaś
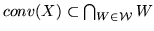 .
.
Dowód. Jest oczywiste, że zbiór
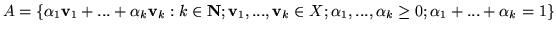 zawiera
zawiera 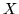 (aby otrzymać wszystkie elementy
zbioru
(aby otrzymać wszystkie elementy
zbioru 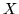 wystarczy położyć we wzorze na
wystarczy położyć we wzorze na 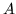
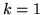 i
i 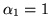 ).
).
Łatwo także wykazać, że 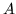 jest zbiorem wypukłym. Rzeczywiście, weźmy
jest zbiorem wypukłym. Rzeczywiście, weźmy
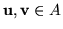 .
Wykażemy, że dla wszystkich
.
Wykażemy, że dla wszystkich
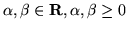 i takich, że
i takich, że
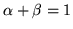 ,
,
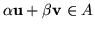 .
.
Skoro
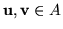 , to istnieją
, to istnieją
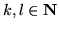 oraz
oraz
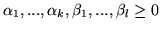 oraz
oraz
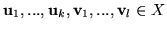 takie, że
takie, że
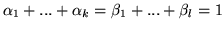 i
i
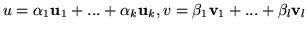 .
.
Wtedy
Tak więc
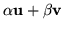 jest kombinacją wektorów
jest kombinacją wektorów
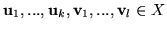 .
Co więcej, współczynniki tej kombinacji są oczywiście nieujemne i
.
Co więcej, współczynniki tej kombinacji są oczywiście nieujemne i
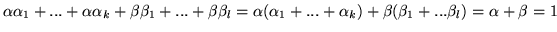 . Czyli
. Czyli
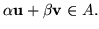
Dla udowodnienia prawdziwości wniosku ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) pozostaje jeszcze wykazać,
że A jest najmniejszym zbiorem
wypukłym zawierającym X czyli, że dla każdego zbioru wypukłego
pozostaje jeszcze wykazać,
że A jest najmniejszym zbiorem
wypukłym zawierającym X czyli, że dla każdego zbioru wypukłego 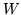 zawierającego
zawierającego 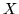 zachodzi
zachodzi
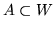 .
.
Niech 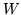 będzie zbiorem wypukłym,
będzie zbiorem wypukłym, 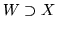 i niech
i niech 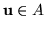 .
Istnieją wobec tego
.
Istnieją wobec tego
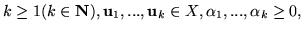 takie, że
takie, że
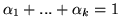 i
i
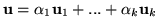 . Korzystając z indukcji
matematycznej ze względu na
. Korzystając z indukcji
matematycznej ze względu na 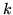 wykażemy, że
wykażemy, że  .
.
Dla 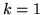 zachodzi uczywiście
zachodzi uczywiście 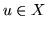 i wobec
i wobec 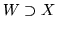 zachodzi także
zachodzi także 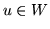 .
Przypuśćmy, że
.
Przypuśćmy, że 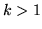 i nasza teza jest prawdą dla
i nasza teza jest prawdą dla 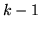 , to znaczy że każda kombinacja
, to znaczy że każda kombinacja
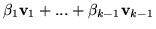 w której
w której
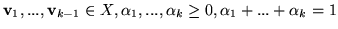 , należy do
, należy do  .
.
Możemy założyć, że
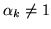 (w przeciwnym przypadku
(w przeciwnym przypadku
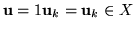 ). Mamy
). Mamy
Oczywiście
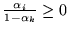 dla
dla 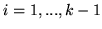 . Co więcej,
. Co więcej,
Stąd i z założenia indukcyjnego
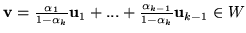 .
.
Ponieważ 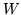 jest z założenia zbiorem wypukłym
jest z założenia zbiorem wypukłym
co kończy dowód wniosku ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) .
Wniosek
.
Wniosek ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) posłuży nam do wykazania poniżej twierdzenia
Carathéodory'ego które mówi, że
w przestrzeni
posłuży nam do wykazania poniżej twierdzenia
Carathéodory'ego które mówi, że
w przestrzeni 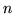 wymiarowej
wymiarowej 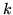 we wniosku
we wniosku ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) można zastąpić przez
można zastąpić przez 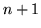 .
.
Dowód. Z wniosku ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) wynika, że jeśli istnieją
wynika, że jeśli istnieją 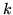 ,
,
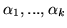 oraz
oraz
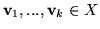 spełniające
spełniające
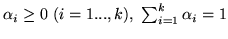 ,
takie, że
,
takie, że
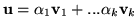 to
to
 (w szczególności wtedy gdy
(w szczególności wtedy gdy 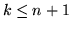 ).
).
Wystarczy więc wykazać, że jeśli
 ,
to istnieje nie więcej niż
,
to istnieje nie więcej niż 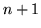 wektorów
wektorów
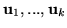 i skalarów
i skalarów
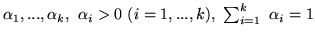 , takich, że
, takich, że
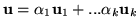 . Dzięki wnioskowi
. Dzięki wnioskowi
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) wiemy, że istnieje
wiemy, że istnieje 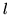 , wektory
, wektory
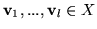 oraz współczynniki
oraz współczynniki
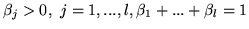 takie, że
takie, że
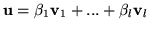 .
.
Zauważmy teraz, że równania
|
(7.1) |
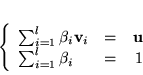 |
dają nam układ 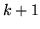 równań rzeczywistych liniowych, których zmiennymi są
równań rzeczywistych liniowych, których zmiennymi są
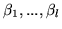 a współczynnikami współrzędne wektorów
a współczynnikami współrzędne wektorów
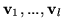 (i jedynki w ostatnim równaniu), zaś
wyrazami wolnymi są współrzędne wektora
(i jedynki w ostatnim równaniu), zaś
wyrazami wolnymi są współrzędne wektora 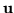 (i jedynka w ostatnim równaniu).
(i jedynka w ostatnim równaniu).
Nasz nieoceniony wniosek ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) zapewnia nam, że układ (
zapewnia nam, że układ (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) jest
niesprzeczny.
Z twierdzenia
) jest
niesprzeczny.
Z twierdzenia ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) wynika więc, że ma nieujemne (!)
rozwiązanie w którym zmiennych bazowych
jest
wynika więc, że ma nieujemne (!)
rozwiązanie w którym zmiennych bazowych
jest 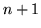 (tyle ile równań). Pamiętamy także, że zmienne
niebazowe w rozwiązaniu bazowym
przyjmują wartość zero. To kończy dowód twierdzenia
(tyle ile równań). Pamiętamy także, że zmienne
niebazowe w rozwiązaniu bazowym
przyjmują wartość zero. To kończy dowód twierdzenia ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) .
.





Next: Układy nierówności i równań
Up: Interpretacje i zastosowania
Previous: Komentarz
Spis rzeczy
Indeks