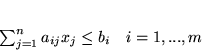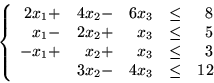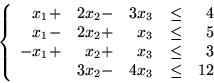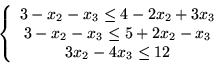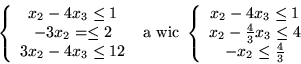Metoda Fouriera-Motzkina
redukcji układów nierówności

Niech będzie dany układ nierówności

$$\sum_{j=1}^n a_{ij}x_j \leq b_i \ \ \ i=1,...,m$$ (7.8)

Metoda Fouriera-Motzkina polega na stopniowej redukcji zmiennych tak, by w końcu otrzymać jedną zmienną niezależną, a więc układ trywialny. Powiedzmy od razu, że to zmniejszanie liczby zmiennych będzie sie odbywało kosztem bardzo szybkiego wzrostu liczby nierówno.sci.
bez straty ogólności można przyjąć, że w układzie ()

-

pierwszych $m_1$ zmiennych ma przy $x_1$ współczynnik dodatni,

-

następne $m_2$ nierówności mają przy $x_1$ współczynnik ujemny, zaś

-

w pozostałych $m-(m_1+m_2)$ nierównościach współczynnik przy $x_1$ jest równy zero.

Dzieląc każdą z $m_1+m_2$ nierówności przez $\mid a_{i1}\mid \ (i=1,...,m_1+m_2)$ otrzymamy z () równoważny mu układ postaci

$$\left\{ \begin{array}{rrcrl} x_1 + & \sum_{j=2}^na_{ij}'... ...}'x_j & \leq & b_i' & i=m_1+m_2+1,...,m \end{array} \right.$$ (7.9)

czyli

$$\left\{ \begin{array}{rrcrl} x_1 + & \sum_{j=2}^na_{ij}'... ...'x_j & \leq & b_i'' & i=m_1+m_2+1,...,m \end{array} \right.$$ (7.10)

gdzie $a_{ij}''=a_{ij}'$ i $b_i''=b_i'$ dla $i=1,...,m_1$ i $i=m_1+m_2+1,...,m$ oraz $a_{ij}''=-a_{ij}'$ i $b_i''=-b_i'$ dla $i=m_1+1,...,m_1+m_2$.
Układ () jest z kolei równoważny

$$\left\{ \begin{array}{cl} b_{i_{1}}'' - \sum_{j=2}^na_{i... ...x_j \leq b_j'' , \ \ i=m_1+m_2+1,...,m \end{array} \right.$$ (7.11)

Zredukowane zadanie będzie następującym układem nierówności:

$$\left\{ \begin{array}{rcll} \sum_{j=2}^na_{i_{2}j}'' - a... ...j}''x_j & \leq & b_i'' & i=m_1+m_2+1,...,m \end{array}\right.$$ (7.12)

Sprzeczność układu () oznacza sprzeczność układu (). Natomiast jeśli układ () jest niesprzeczny to tażde rozwiązanie $x_2,...,x_n$ można rozszerzyć do rozwiązania $x_1,x_2,...,x_n$ dołączając dowolne $x_1$ spełniające ().
Zobaczymy jak opisana metoda funkcjonuje na przykładzie.

Przykład 7.6   Niech będzie danu układ równań

$$\left\{ \begin{array}{rrrrr} 2x_1+ & 4x_2 - & 6x_3 & \leq... ...& \leq & 3\\ & 3x_2- & 4x_3 & \leq & 12 \end{array} \right.$$

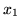
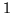
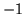
Zastosujmy do tego układu kolejne etapy metody Fouriera-Motzkina. Po pierwsze, doprowadzamy do sytuacji w której współczynniki przy $x_1$ są równe $1$, $-1$ lub $0$

$$\left\{ \begin{array}{rrrrr} x_1+ & 2x_2 - & 3x_3 & \leq ... ...& \leq & 3\\ & 3x_2- & 4x_3 & \leq & 12 \end{array} \right.$$

Stąd

$$\left\{\begin{array}{c} 3-x_2-x_3 \leq x_1 \leq 4 - 2x_2 ... ... 5 + 2x_2 - x_3 \\ 3x_2 - 4x_3 \leq 12 \end{array} \right.$$ (7.13)

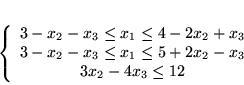i zredukowany układ nierówności

$$\left\{\begin{array}{c} 3-x_2-x_3 \leq 4-2x_2+3x_3\\ 3 - x_2-x_3 \leq 5+2x_2-x_3\\ 3x_2-4x_3\leq 12 \end{array}\right.$$

który po zredukowaniu przyjmie postać

$$\left\{\begin{array}{c} x_2-4x_3\leq 1\\ -3x_2 = \leq 2\\ ... ...{4}{3}x_3 \leq 4\\ -x_2 \leq \frac{4}{3} \end{array}\right.$$

Teraz redukujemy zmienną $x_2$:

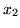
$$\left\{\begin{array}{c} -\frac{2}{3} \leq x_2 \leq 1+4x_3... ...frac{2}{3} \leq x_2 \leq 4 + \frac{4}{3}x_3 \end{array}\right.$$ (7.14)

$$\left\{\begin{array}{c} -4x_3 \leq \frac{5}{3}\\ -\frac{4}{3} x_3 \leq \frac{14}{3} \end{array}\right.$$

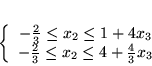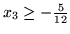
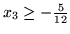
i ostatecznie $x_3 \geq -\frac{5}{12}$. Ten wynik zaś oznacza, że dla każdego $x_3 \geq -\frac{5}{12}$ możemy dzieki () i () znaleźć odpowiednie wartości $x_2$ i $x_3$.

Zauważmy, że przy układzie co najwyżej trzech nierówności liczba nierówności przy kolejnych redukcjach nie zwiększa się (tak właśnie było w naszym przykładzie). Rozwiązując samodzielnie następne ćwiczenia czytelnik zauważy, że liczba nierówności na ogół rośnie bardzo szybko w miarę kolejnych redukcji. Więcej o redukcji układów nierówności w [19].
Metoda eliminacji Fouriera-Motzkina daje nam inny algorytm rozwiązywania PPL. Rzeczywiście, niech będzie dany PPL

$$\left\{\begin{array}{l} {\bf Ax} \leq {\bf b}\\ \hline\\ {\bf cx} \rightarrow \max \end{array} \right.$$ (7.15)

W celu znalezienia rozwiązania optymalnego dla () zastosujmy metodę redukcji do układu

$$\left\{\begin{array}{l} {\bf Ax} \leq {\bf b}\\ \lambda -{\bf cx} \leq 0 \end{array} \right.$$ (7.16)

gdzie $\lambda$ jest nową zmienną. Redukować będziemy kolejne współrzędne wektora ${\bf x}$ tak, że w końcu pozostanie nam tylko zmienna $\lambda$. Teraz wystarczy przyjąć $\lambda$ największą możliwą, by otrzymać rozwiązanie optymalne problemu ().
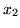
Zauważmy na koniec, że metodę Fouriera-Motzkina można stosować także do redukowania układów w których występują także silne nierówności.
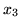