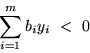Układy nierówności i równań liniowych

Niniejszy ustęp poświęcimy twierdzeniu Kuhna dotyczącemu układów nierówności i równań liniowych które udowodnimy metodami programowania liniowego. Już w następnym ustępie będziemy z tego twierdzenia korzystać w dowódzie twierdzenia o rozdzielaniu (twierdzenie ).
Układem równań i nierówności liniowych będziemy nazywać układ postaci

$$\left\{ \begin{array}{lclr} \sum_{j=1}^n a_{ij}x_j & \le... ...1}^n a_{ij}x_j & = & b_i & (i \in R)\\ \end{array} \right.$$ (7.2)

gdzie $N \cup R =\{ 1,...,m\}$.
Z tej postaci nierównościami zetknęliśmy się już w ustępie z tą niewielką różnicą, że tym razem nie wyróżniamy specjalnie nierówności postaci
$x_j\geq 0$, które mogą występować jako specjalne przypadki nierówności postaci $\sum_{j=1}^n a_{ij}x_j \leq b_i$.
Tak jak już to robiliśmy wielokrotnie, możemy i tym razem wymnożyć każdą z nierówności $\sum_{j=1}^n a_{ij}x_j \leq b_i$ przez nieujemne $y_i$ otrzymując

$$\begin{array}{lclr} (\sum_{j=1}^n a_{ij}x_j)y_i & \leq & y_i b_i & (i \in N) \end{array}$$

oraz każdą z równości $\sum_{j=1}^n a_{ij}x_j = b_i$ przez, tym razem dowolne $y_i$ otrzymując

$$\begin{array}{lclr} (\sum_{j=1}^n a_{ij}x_j)y_i & = & y_i b_i & (i \in R) \end{array}$$

by po zsumowaniu po $i=1,...,m$ a następnie zmienieniu kolejności sumowania po prawej stronie nierówności otrzymać

$$\begin{array}{lclr} \sum_{j=1}^n(\sum_{i=1}^m a_{ij}y_i)x_j & \leq & \sum_{i=1}^m y_i b_i \end{array}$$ (7.3)

Zwróćmy uwagę, że w ten prosty sposób otrzymaliśmy pewne kryterium niesprzeczności układu (). Nim kryterium to sformułujemy w postaci ogólnej, przyjrzymy się jak funkcjonuje ono na przykładzie.

Przykład 7.5   Niech będzie dany następujący układ nierówności i równań liniowych:

$$\left\{ \begin{array}{rcrcrcrcr} 2x_1 & - & 7x_2 & +& x_... ... & + & 2x_2 & +& 2x_3 & + & 2x_4 & = & 6 \end{array} \right.$$ (7.4)

Jeśli w nierówności podstawimy $y_1=1,\ y_2=2,\ y_3=3$ i $y_4=-1$, wtedy otrzymamy $0x_1+0x_2+0x_3-0x_4 \leq -1$ (a więc sprzeczność), przy czym tylko zmienna odpowiadająca równości ($y_4$) przyjmuje wartość ujemną ($y_4=-1$). Stąd wniosek, że nasz układ jest sprzeczny.

Definicja 7.3   Mówimy, że układ jest niezgodny jeśli istnieją liczby $y_1,...,y_m$ spełniające następujące warunki

$$\left\{ \begin{array}{rcrcl} y_i & \geq & 0 & \mbox{ dla... ...1,...,n\\ \sum_{i=1}^m b_iy_i & < & 0 \end{array} \right.$$ (7.5)

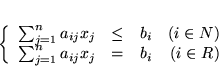Wobec tego co powiedziano wyżej jest zupełnie oczywiste, że jeśli układ jest niezgodny, to jest sprzeczny. Okazuje się, że zależność pomiędzy niezgodnością a sprzecznością układu jest znacznie głębsza i niebanalna. Prawdziwe jest bowiem następujące twierdzenie, udowodnione przez H.W. Kuhna w 1956 roku.

Twierdzenie 7.5 (Kuhn)   Układ nierówności i równań liniowych () jest sprzeczny wtedy i tylko wtedy, jeżeli jest niezgodny.

Dowód. Po tym co już zostało powiedziane, wystarczy udowodnić, że jeżeli układ jest sprzeczny, to jest także niezgodny.
Rozważmy następujący problem programowania liniowego

$$% latex2html id marker 8079 \left\{ \begin{array}{rllllr... ...\ x_{n+i} & \geq & 0 & (i=1,...,m) \end{array} \right.$$ (7.6)

gdzie

$$w_{n+i}= \left\{ \begin{array}{rcl} 1 & \mbox{ gdy } & b_i \geq 0\\ -1 & \mbox{ gdy } & b_i < 0 \end{array} \right.$$

Jest oczywiste, że układ () jest niesprzeczny wtedy i tylko wtedy, gdy () posiada rozwiązanie optymalne które ma wartość zero (co może mieć miejsce jedynie jeśli $x_{n+1}=...=x_{n+m}=0$). Nasz problem () jest oczywiście niesprzeczny ( $x_i=0, \ x_{n+i}=\mid b_i\mid$ dla $i=1,...,m$ są rozwiązaniem) i ograniczony (nie ma rozwiązania o wartości mniejszej, ani równej zero). Rozwiązanie optymalne istnieje więc na mocy twierdzenia , skoro zaś () jest układem sprzecznym, wartość optymalnego rozwiązania PPL () jest ujemna. Zauważmy, że minimalizacja funkcji $\sum_{i=1}^mx_{n+i}$ jest równoważna maksymalizacji $\sum_{i=1}^m(-x_{n+i})$. Tak więc problemem dualnym do () jest

$$% latex2html id marker 8116 \left\{ \begin{array}{rcrl} ... ... i=1,...,m\\ y_i & \geq & 0 & i \in N \end{array} \right.$$ (7.7)

Jeżeli układ nierówności i rownań liniowych () jest sprzeczny, to optymalna wartość funkcji celu $\sum_{i=1}^m(-x_{n+i})$ jest ściśle ujemna, a stąd na mocy ogólnej zasady dualności (twierdzenie )

$$\sum_{i=1}^mb_iy_i \ < \ 0$$

Ta ostatnia nierówność łącznie z ograniczeniami problemu () oznacza, że system () jest niezgodny.