Definicja 7.4
Niech
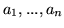
będą liczbami rzeczywistymi nie równymi równocześnie zero
(inaczej:
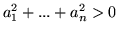
). Zbiór wektorów
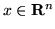
o współrzędnych
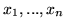
spełniających
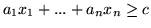
(gdzie
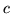
jest pewną liczbą rzeczywistą
nazywamy
półprzestrzenią.
Wielościanem w
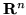
nazywamy
przecięcie skończonej liczby półprzestrzeni.
Twierdzenie 7.6 (O rozdzielaniu wielościanów)
Dla dowolnych wielościanów
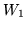
i
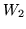
rozłącznych i niepustych,
istnieją rozłączne
półprzestrzenie
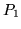
i
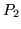
takie, że
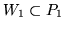
i
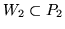
.