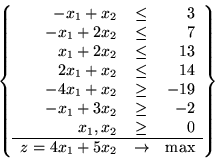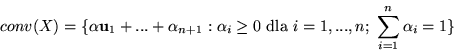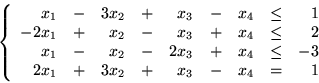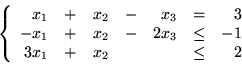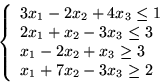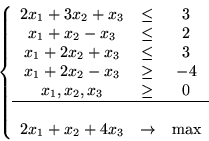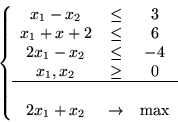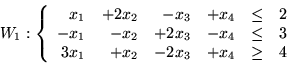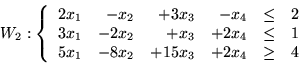Next: Metody sieciowe
Up: Interpretacje i zastosowania
Previous: Wielościany i półprzestrzenie
Spis rzeczy
Indeks
Ćwiczenie 7.1
Niech będzie dany PPL
- (a)
- Napisz postać standardową i kanoniczną tego problemu.
- (b)
- Podaj jego interpretację geometryczną (wykonaj rysunek).
Nie stosując algorytmu sympleks:
- (c)
- Znajdź rozwiązanie optymalne. Czy istnieje tylko jedno optymalne rozwiązanie
tego problemu?
- (d)
- Zakładając, że wybór zmiennej wchodzący dokonowany jest tak jak zazwyczaj
(tj. zmienną wchodzącą jest
ta której dodatni współczynnik w funkcji celu jest największy). podaj rozwiązania
bazowe każdej iteracji.
- (e)
- To samo pytanie przy wyborze zmiennej wchodzącej regułą Blanda.
W (d) i (e) zakładamy, że pierwszym rozwiązaniem bazowym jest 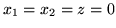
(w rozwiązaniach bazowych należy podać wartości
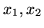
i
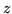
).
Ćwiczenie 7.4
Metodą Fouriera-Motzkina zredukuj układy nierówności z
ćwiczeń
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
i
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
niniejszego rozdziału.
Ćwiczenie 7.5
Korzystając z metody Fouriera-Motzkina
znajdź optymalne rozwiązania problemów:
Ćwiczenie 7.6
Wykaż, że dla każdego zbioru skończonego
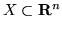
powłoką
wypukłą jest przedział domknięty.
Ćwiczenie 7.7
Udowodnij, że każdy wielościan jest zbiorem wypukłym.
Ćwiczenie 7.8
Wskaż przykłady dowodzące, że w twierdzeniu
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
wielościanów nie da się zastąpić
zbiorami wypukłymi.





Next: Metody sieciowe
Up: Interpretacje i zastosowania
Previous: Wielościany i półprzestrzenie
Spis rzeczy
Indeks