




Next: Twierdzenie Mengera
Up: Metody sieciowe
Previous: Zbiór różnych reprezentantów
Spis rzeczy
Indeks
Zanim powiemy jak powiemy jak uogólnić twierdzenie ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) dla dowolnych
grafów (niekoniecznie dwudzielnych), powiedzmy jak poradzić sobie z problemem
maksymalnego przepływu w sieci w której poza ograniczeniami na przepustowości
łuków dane są także przepustowości wierzchołków.
dla dowolnych
grafów (niekoniecznie dwudzielnych), powiedzmy jak poradzić sobie z problemem
maksymalnego przepływu w sieci w której poza ograniczeniami na przepustowości
łuków dane są także przepustowości wierzchołków.
Mamy wtedy następujący problem:
Dla danej sieci
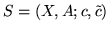 , gdzie
, gdzie
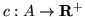
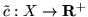 o źródle
o źródle 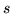 i
odpływie
i
odpływie 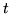 znaleźć funkcję
znaleźć funkcję
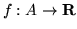 spełniającą
spełniającą
zmaksymalizować
Rozwiązanie powyższego problemu8.18
otrzymujemy bardzo łatwo korzystając z poznanej
już metody dla sieci bez ograniczeń przepustowości wierzchołków.
Tworzymy nową sieć 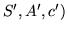 w której każdy wierzchołek
w której każdy wierzchołek 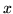 zastępujemy
dwoma wierzchołkami
zastępujemy
dwoma wierzchołkami 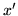 i
i 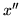 .
.
Zbiór łuków 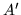 i przepustowości definiujemy następująco:
i przepustowości definiujemy następująco:
-
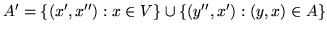 ,
,
-
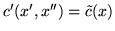 dla każdego
dla każdego 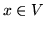 ,
,
-
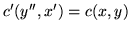 jeśli
jeśli 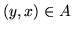
Jest oczywiste, że wartość maksymalnego przepływu 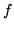 w sieci
w sieci  ze
źródła
ze
źródła 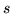 do odpływu
do odpływu 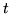 jest równa wartości maksymalnego
jest równa wartości maksymalnego 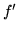 przepływu
w
przepływu
w 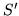 ze źródła
ze źródła 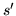 do odpływu
do odpływu 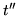 .
.
Oczywistym jest także, że 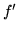 można znaleźć przy pomocy
algorytmu Forda-Fulkersona i w łatwy
sposób sprowadzić potem do przepływu
można znaleźć przy pomocy
algorytmu Forda-Fulkersona i w łatwy
sposób sprowadzić potem do przepływu 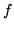 w sieci
w sieci  .
.





Next: Twierdzenie Mengera
Up: Metody sieciowe
Previous: Zbiór różnych reprezentantów
Spis rzeczy
Indeks