Zbiór różnych reprezentantów

Niech będzie dany zbiór $X$ i pewna rodzina podzbiorów $\cal{X}$ tego zbioru. Kiedy istnieje zbiór $Y \subset X$ taki, że istnieje różnowartościowa funkcja $g: \cal{X}\ \rightarrow Y$? Jeśli taki zbiór $Y$ istnieje, nazywamy go zbiorem różnych reprezentantów rodziny $\cal{X}$.

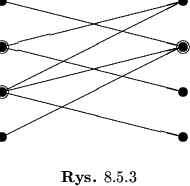
Przykład 8.5   W sejmie, senacie^8.15 istnieją różne komisje zajmujące się różnymi problemami ^8.16. Komisje te kędziemy traktowali jako podzbioru zbioru posłów (lub senatorów). Każda komisja ma swojego przewodniczącego. Wygodnie jest by przewodniczącymi róznych komisji były różne osoby. Powstaje więc problem: jak powinny być dobrane komisje by mogło tak być?

Problem istnienia zbioru różnych reprezentantów można przetłumaczyć na język teorii grafów następująco:
Niech każdemu zbiorowi $X_i \in {\cal X}$ odpowiada wierzchołek $x_i$ i niech $A=\{ x_i: X_i \in \cal{X}\}$, oraz $B=X$. Niech teraz $G$ bedzie grafem dwudzielnym $G=(A,B;E)$ takim, że $E=\{X_ix: x \in X_i\}$. Problem istnienia zbioru różnych reprezentantów rodziny $\cal{X}$ jest równoważny istnieniu w $G$ skojarzenia pełnego zbioru $A$. Stąd i z twierdzenia wynika bardzo łatwo następujący wniosek.

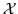
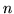
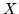
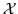
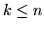
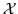
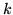
Wniosek 8.8 (Hall)   [12] Niech $\cal{X}$ będzie rodziną $n$ podzbiorów zbioru $X$. Zbiór różnych reprezentantów rodziny $\cal{X}$ istnieje wtedy i tylko wtedy, gdy unia dowolnych $k\le n$ zbiorów rodziny $\cal{X}$ zawiera co najmniej $k$ elementów.

Następne, słynne twierdzenie Königa-Egerváry'ego, zostało opublikowane w książce Königa [15] której ukazanie się w 1936 roku stało się, jak się powszechnie uważa, aczynem" trwającego do dziś bardzo intensywnego rozwoju teorii grafów^8.17.

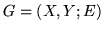
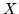
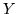
Twierdzenie 8.9 (Königa-Egerváry'ego)   W grafie dwudzielnym $G=(X,Y;E)$ minimalna liczba wierzchołkow w zbiorze rozdzielającym $X$ i $Y$ jest równa liczbie krawędzi w maksymalnym skojarzeniu.

Przykład 8.6   Na rysunku 8.5.3 przedstawiono graf dwudzielny. Sprawdź, że wierzchołki wyróżnione tworzą w nim zbiór rozdzielający i wskaż skojarzenie o trzech krawędziach.

Dowód twierdzenia jest podobny do dowodu twierdzenia . Z grafem $G$ kojarzymy sieć $S=(X',Y';E')$ w identyczny co w dowodzie twierdzenia sposób i zauważamy, że każdemu przekrojowi $(W,\bar{W})$ z $W=A \cup B \cup \{ s\}$, $A \subset X, B\subset Y,$ o przepustowości w $S$ równej, jak widzieliśmy, $\mid X - A \mid +\linebreak\mid B \mid$, odpowiada zbiór rozdzielający $(X-A)\cup B$ który też ma $\mid X - A \mid + \mid B \mid$ wierzchołków.