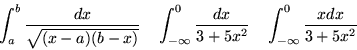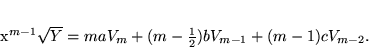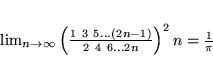Next: Algebra i geometria analityczna
Up: Zadania z matematyki dla
Previous: Rachunek różniczkowy funkcji jednej
Contents
- Oblicz następujące całki nieoznaczone:
- Wykaż, ze jezeli
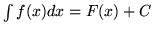 , wtedy
, wtedy
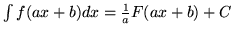 .
.
- Oblicz:
- Metodą podstawiania oblicz następujące całki :
- W tym zadaniu nauczymy się (trochę inaczej) całkować
funkcje postaci
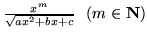 , a w
konsekwencji funkcje postaci
, a w
konsekwencji funkcje postaci
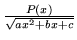 , gdzie P(x)
jest pewnym wielomianem.
, gdzie P(x)
jest pewnym wielomianem.
Oznaczmy
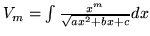 ,
oraz
,
oraz 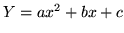 .
.
- (a)
- Licząc pochodną wyrażenia
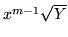 a następnie
całkując stronami wykaż wzór
a następnie
całkując stronami wykaż wzór
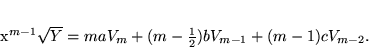 |
(6.1) |
- (b)
- Korzystając z (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) wyraź
) wyraź 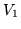 i następnie
i następnie 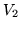 przez
przez 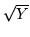 i
i 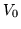 .
.
- (c)
- Kontynuując to postępowanie wywnioskuj, ze
gdzie 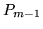 jest wielomianem stopnia
jest wielomianem stopnia
![\(m-1ża\'s \(\lambda_{m}\)
pewną stałą.
\item[{{(d)}}]
Wielomian \(P_{m}\)i s...
...frac{dx}{(x-\alpha)^k\sqrt{Y}}żacznij
od podstawienia \(x-\alpha=\frac1t\).](img264.gif)
- Przyjmując podstawienia trygonometryczne :
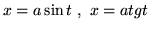 ,
,
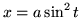 i t.p. oblicz:
i t.p. oblicz:
- Oblicz:
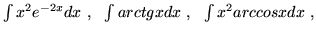
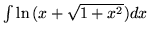
- Sporządź wykresy funkcji :
(a)
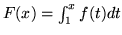 jeżeli
jeżeli
(b)
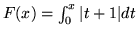 .
.
- Oblicz
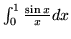 z dokładnością do 0,001.
z dokładnością do 0,001.
- Celem zadania jest wykazanie wzoru Wallisa:
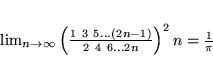 |
(6.2) |
Niech
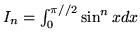 , dla
, dla
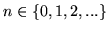
- (a)
- Oblicz
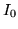 oraz
oraz 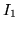 .
.
- (b)
- Korzystając ze wzoru na całkowanie przez częsci,
wykaż, że
- (c)
- Z (a) i (b) wywnioskuj, ze
- (d)
- Jednym zdaniem uzasadnij nierównosci :
dla
![\(x\in{[0,\pi//2]}.\)](img282.gif)
- (e)
- Zacytuj twierdzenie, z którego wynikają nierównosci
- (f)
- wydedukuj stąd granicę
- (a)
- granicę
i
- (h)
- wzór Wallisa (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ).
).
- Niech
 będzie funkcją ciągłą z R w R ,
będzie funkcją ciągłą z R w R ,
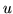 i
i 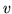 dwiema funkcjami rózniczkowalnymi z R w R i niech
dwiema funkcjami rózniczkowalnymi z R w R i niech
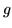 będzie funkcją zdefiniowaną wzorem
będzie funkcją zdefiniowaną wzorem
- (a)
- Wykaż, że
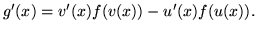
- (b)
- Niech G będzie funkcją zdefiniowaną przez
Oblicz G'(x).
- Oblicz pole figury płaskiej ograniczonej krzywymi
- (a)
-
![\( y=\sin x\ , \ y=\cos x\ \ ;\ \ x\in{[\frac{\pi}{4},\frac{5\pi}{4}]}\)](img291.gif)
- (b)
-
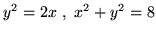
- (c)
-
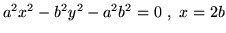
- (d)
-
![\( y=x\ , \ y=\sin^2x+x \ \ ;\ \ x\in{[0,\pi]}\)](img294.gif)
- (e)
-
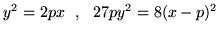
- Oblicz pole figury ograniczonej
- (a)
- łukiem o równaniach
osią 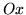 i osią
i osią 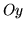 .
.
- (b)
-
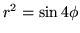
- (c)
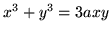
- (d)
-
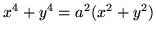
- Oblicz długosc łuku
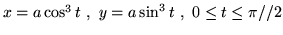
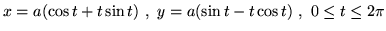
- Oblicz objętosc bryły powstałej
przez obrót obszaru ograniczonego przez krzywą
- (a)
-
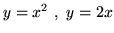 wokół osi
wokół osi 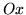
- (b)
-
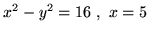 wokół osi
wokół osi 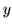 .
.
- Oblicz współrzędne srodka cięzkosci
- (a)
- łuku cykloidy
jesli gęstosc masy
jest na tym łuku stała.
- (b)
- łuku okręgu
jesli gęstosc liniowa masy rozłozonej
na tym łuku
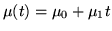 .
.
- Oblicz pole powierzchni bocznej
bryły powstałej przez :
- obrót o 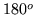 wokół osi OX elipsy
wokół osi OX elipsy
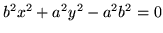
- obrót krzywej
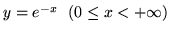 wokół osi OY.
wokół osi OY.
- Rozciągnięcie spręzyny o 1 cm wymaga przyłozenia siły 1 N.
Oblicz pracę ,
którą trzeba wykonac by rozciągnąc tę spręzynę
do 5 cm .
- Zbadaj zbieznosc i ew. oblicz całki
niewłasciwe




Next: Algebra i geometria analityczna
Up: Zadania z matematyki dla
Previous: Rachunek różniczkowy funkcji jednej
Contents
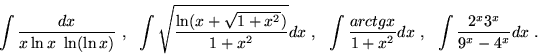
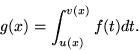
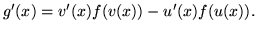
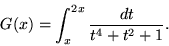
![\( y=\sin x\ , \ y=\cos x\ \ ;\ \ x\in{[\frac{\pi}{4},\frac{5\pi}{4}]}\)](img291.gif)
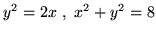
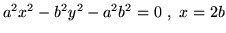
![\( y=x\ , \ y=\sin^2x+x \ \ ;\ \ x\in{[0,\pi]}\)](img294.gif)
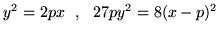
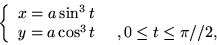
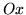 i osią
i osią 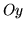 .
.
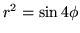
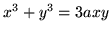
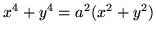
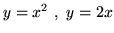 wokół osi
wokół osi 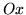
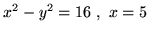 wokół osi
wokół osi 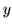 .
.
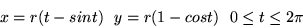
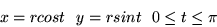
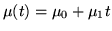 .
.