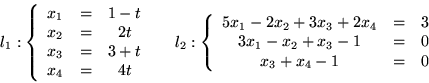- W
 definiujemy działanie wewnętrzne
definiujemy działanie wewnętrzne  Sprawdź, czy działanie to jest przemienne? łączne? Czy
ma element neutralny? Czy dowolny element
Sprawdź, czy działanie to jest przemienne? łączne? Czy
ma element neutralny? Czy dowolny element 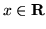 ma element
odwrotny ze względu na
ma element
odwrotny ze względu na 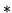 ?
?
- Wykaż, że w dowolnej grupie
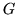
istnieje tylko jeden element neutralny,
dla dowolnego elementu istnieje tylko jeden element odwrotny.
- Które z poniższych zbiorów są przestrzeniami
wektorowymi:
(z działaniami jak w 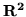 ).
).
(z działaniami jak w
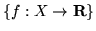 ,
, 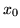 jest
pewnym elementem (niepustego) zbioru
jest
pewnym elementem (niepustego) zbioru 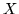 ).
).
- Wykaż, że w dowolnej przestrzeni wektorowej
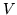 nad
ciałem
nad
ciałem 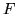 zachodzą związki:
zachodzą związki:
mmmmmmmmmmmmmmmmm
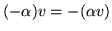
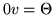
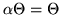
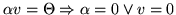
(gdzie 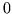 jest elementem neutralnym dla dodawania w ciele
jest elementem neutralnym dla dodawania w ciele 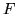 , zaś
, zaś
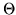 wektorem zerowym, tzn. elementem neutralnym dla dodawania w
przestrzeni wektorowej V).
wektorem zerowym, tzn. elementem neutralnym dla dodawania w
przestrzeni wektorowej V).
- Które z poniższych zbiorów są podprzestrzeniami
przestrzeni wektorowej
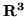 ?
?
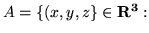
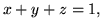
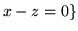
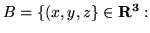
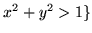
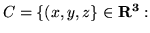
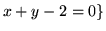
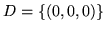
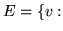
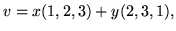
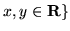
- Niech
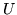 i
i 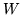 będą podprzestrzeniami przestrzeni
wektorowej
będą podprzestrzeniami przestrzeni
wektorowej 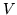 nad ciałem
nad ciałem 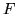 . Które z poniższych zbiorów
są podprzestrzeniami wektorowymi ?
. Które z poniższych zbiorów
są podprzestrzeniami wektorowymi ?
(a) 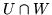 (b)
(b) 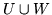
(c) 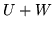
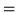
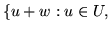
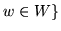
(d) 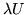
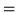
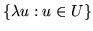
- Sprawdż liniową zależność zbiorów:
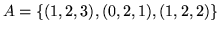 w
w 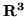
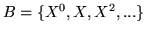 w
w ![${\bf R[X]}$](img360.gif)
![$C=\left\{ \left[ \begin{array}{cc} 1 & 2\\ 0 & 1\end{array} \right] ,
\left[ \...
... \right] ,
\left[ \begin{array}{cc} 0 & 2\\ 2 & 0\end{array} \right] \right\} $](img361.gif) in
in
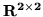 .
.
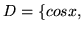
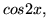
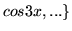 w
w 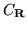 (zbiór
funkcji ciągłych zbioru
(zbiór
funkcji ciągłych zbioru 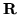 w
w 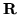 ).
).
- Wykaż, że:
(a) każdy zbiór zawierający wektor 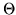 jest
liniowo zależny,
jest
liniowo zależny,
(b) każdy zbiór zawierający zbiór liniowo zależny jest
liniowo zależny.
Sformułuj i udowodnij odpowiednie stwierdzenie dla zbiorów
liniowo niezależnych.
- Znajdź bazę przestrzeni
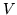 zawierającą wektory
zawierającą wektory
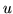 i
i 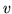 , jeżeli
, jeżeli
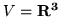 ,
, 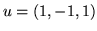 ,
, 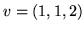
![$V={\bf R^3}[X]$](img370.gif) ,
, 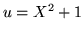 ,
, 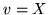
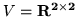 ,
,
![$u=\left[ \begin{array}{cc} 1 & 1 \\ 1 & 1
\end{array} \right] $](img374.gif) ,
,
![$v=\left[ \begin{array}{cc} 1 & 0 \\ 1 & 1 \end{array} \right]$](img375.gif)
- Zbiór
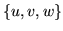 jest bazą przestrzeni
jest bazą przestrzeni 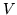 . Wykaż,
że
. Wykaż,
że
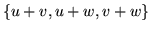 jest także bazą przestrzeni
jest także bazą przestrzeni 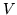 .
.
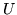 i
i 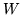 są podprzestrzeniami przestrzeni wektorowej
są podprzestrzeniami przestrzeni wektorowej 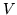 .
Wykaż, że
.
Wykaż, że
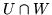 oraz
oraz 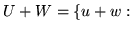
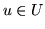 ,
, 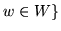
są podprzestrzeniami wektorowymi.
Udowodnij, że jeśli 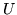 i
i 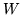 są skończenie wymiarowe, to
są skończenie wymiarowe, to
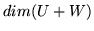
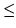
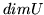
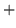
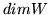 oraz
oraz
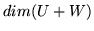 =
= 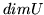 +
+ 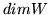
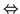
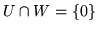 .
.
- Które z poniższych odwzorowań są, a które nie
są liniowe ?
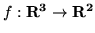 ,
,
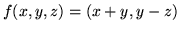
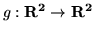 ,
,
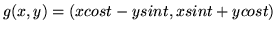
![$h:{\bf R}[X] \rightarrow {\bf R}[X]$](img390.gif) ,
, 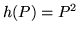
Dla tych funkcji które są liniowe:
(a) Znajdź jądro, obraz, bazy jądra i obrazu oraz wymiary
tych podprzestrzeni.
(b) Wskaż macierze
- w bazach kanonicznych
- w dowolnie wybranych (lecz różnych od kanonicznych) bazach.
- Udowodnij, że odwzorowanie liniowe
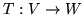 jest
iniektywne wtedy i tylko wtedy gdy
jest
iniektywne wtedy i tylko wtedy gdy 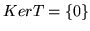 .
.
- Wskaż odwzorowanie liniowe
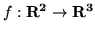 ,
takie że
,
takie że
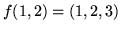 ,
,
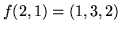 . Znajdź rząd
. Znajdź rząd
 i wymiar
i wymiar 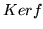 .
.
- Niech
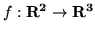 ,
,
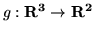 ,
,
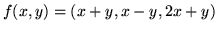 ,
,
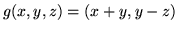 .
.
Sprawdź, że  i
i 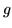 są liniowe. Na dwa sposoby znajdź
macierze
są liniowe. Na dwa sposoby znajdź
macierze 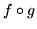 i
i 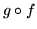 w bazach kanonicznych
w bazach kanonicznych 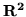 i
i
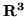 :
:
Wykonując zlożenie funkcji, następnie znajdując macierz
złożenia.
Korzystając z twierdzenia o macierzy złożenia odwzorowań
liniowych.
- Wykaż, że
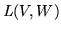 - zbiór odwzorowań
liniowych przestrzeni wektorowej
- zbiór odwzorowań
liniowych przestrzeni wektorowej 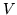 w przestrzeń wektorową
w przestrzeń wektorową 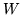 ,
jest przestrzenią wektorową (
,
jest przestrzenią wektorową (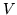 i
i 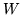 są przestrzeniami nad
wspólnym ciałem
są przestrzeniami nad
wspólnym ciałem 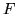 ). Wykaż, że jeśli
). Wykaż, że jeśli
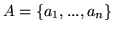 jest bazą
jest bazą 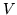 zaś
zaś
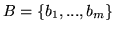 bazą
bazą 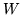 , to zbiór
, to zbiór
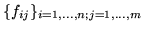 , gdzie
, gdzie
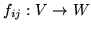 są
takimi odwzorowaniami liniowymi, że
są
takimi odwzorowaniami liniowymi, że
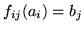 , jest bazą
, jest bazą
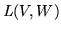 .
.
- Macierzą operatora liniowego
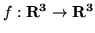 w bazie
kanonicznej
w bazie
kanonicznej
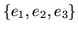 jest
jest
Wykaż, że wektory
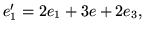
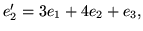
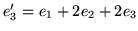 tworzą bazę
tworzą bazę 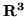 i oblicz macierz
i oblicz macierz
 względem tej bazy.
względem tej bazy.
- Niech
Redukując 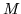 do macierzy trójkątnej oblicz
do macierzy trójkątnej oblicz 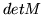
- Wykorzystując odpowiednie twierdzenie o rzędzie
macierzy i wyznacznikach jego podmacierzy wykaż, że wektory
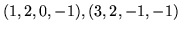 i
i 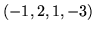 są liniowo niezależne.
są liniowo niezależne.
Następnie sprawdź niezależność tych wektorów
- z definicji
- korzystając z redukcji Gaussa.
-
Wykaż, że dla
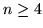
Jaki wynik otrzymamy dla 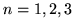 ?
?
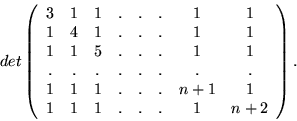
-
Oblicz:
- Wyznacz rzędy macierzy
w zależności od parametru 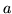 .
.
- Dla jakiej wartości parametru
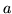 rząd macierzy
rząd macierzy
jest minimalny ?
- Oblicz
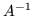 jeżeli
jeżeli
- Rozwiąż następujący układ równań:
- Przedyskutuj rozwiązalność i ew. rozwiąż
w zależności od wartości parametrów
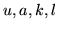 poniższe
układy równań:
poniższe
układy równań:
- Niech
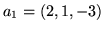 ,
, 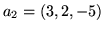 ,
, 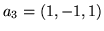 ,
i
,
i 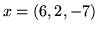 będą wektorami przestrzeni
będą wektorami przestrzeni 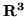 .
.
(a) Sprawdź, że
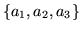 jest bazą
jest bazą 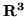 .
.
(b) Znajdź współrzędne wektora 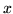 względem tej
bazy.
względem tej
bazy.
Niech
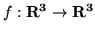 będzie operatorem liniowym
którego macierzą w bazie kanonicznej jest
będzie operatorem liniowym
którego macierzą w bazie kanonicznej jest
(c) Znajdź macierz  w bazie
w bazie
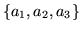 .
.
Uwaga: Punkty (a) i (b) proszę rozwiązać na dwa sposoby
(z wykorzystaniem macierzy przejścia i bez).
- Niech
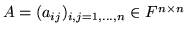 . Skalar
. Skalar
nazywamy śladem macierzy 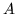 .
.
Wykaż, że macierze podobne mają
(a) ten sam ślad,
(b) ten sam wyznacznik.
Czy podobne są macierze 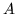 i
i 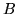 jeżeli
jeżeli
- Na przykładach macierzy z poprzedniego zadania sprawdź
prawdziwość następującego twierdzenia:
Twiedzenie Cayleya-Hamiltona. Dla dowolnej macierzy
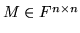 zachodzi
zachodzi 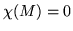 , gdzie
, gdzie 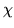 jest
wielomianem charaktrystycznym macierzy
jest
wielomianem charaktrystycznym macierzy 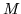 .
.
- Dla każdej z poniższych macierzy sprawdź czy jest
diagonalizowalna. Jeśli tak, to napisz jej postać diagonalną.
- Wskaż bazę w której operator liniowy
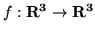 , zdefiniowany wzorem
, zdefiniowany wzorem
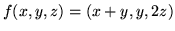 ma macierz diagonalną.
ma macierz diagonalną.
- Wykaż, że
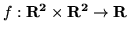 ,
,
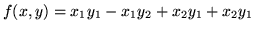 jest formą dwuliniową,
znajdź macierz ją reprezentującą w bazie kanonicznej
i w bazie
jest formą dwuliniową,
znajdź macierz ją reprezentującą w bazie kanonicznej
i w bazie
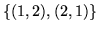 .
.
- Wykaż, że dla dowolnych macierzy
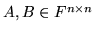 zachodzi
zachodzi 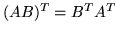 .
.
- Wykaż, że
(a)
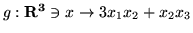
(b)
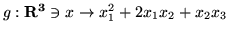
jest formą kwadratową.
Znajdź macierz formy 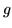 w bazie kanonicznej.
w bazie kanonicznej.
Doprowadź 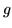 do postaci kanonicznej. Znajdź bazę
do postaci kanonicznej. Znajdź bazę
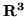 w której
w której 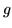 ma postać kanoniczną.
ma postać kanoniczną.
- Zbadaj określoność form kwadratowych których
macierzami są
- Znajdź rozwiązanie ogólne układu równań:
a następnie rozwiązanie spełniające warunek początkowy
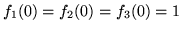 .
.
- Wykaż, że kazda przestrzeń unormowana jest
metryczna. Które z poniższych odwzorowań są normami ?
(a)
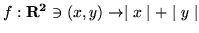
(b)
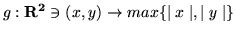
(c)
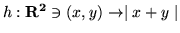
- Dla jakiej wartości parametru
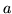 płaszczyzna
płaszczyzna
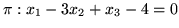 jest równoległa do prostej
jest równoległa do prostej
- Napisz równania płaszczyzn:
- przechodzącej przez 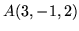 i prostopadłej do wektora
i prostopadłej do wektora
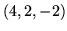
- przechodzącej przez 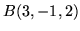 i równoległej do
wektorów
i równoległej do
wektorów 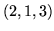 i
i 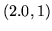 .
.
- Znajdź punkt przecięcia prostej:
i hiperpłaszczyzny:
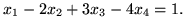
- Znajdź kąt między prostymi
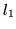 i
i 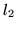 w
w 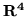
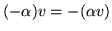
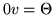
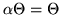
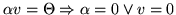
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() (b)
(b) ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() w
w ![]()
![]() w
w ![]()
![$C=\left\{ \left[ \begin{array}{cc} 1 & 2\\ 0 & 1\end{array} \right] ,
\left[ \...
... \right] ,
\left[ \begin{array}{cc} 0 & 2\\ 2 & 0\end{array} \right] \right\} $](img361.gif) in
in
![]() .
.
![]()
![]()
![]() w
w ![]() (zbiór
funkcji ciągłych zbioru
(zbiór
funkcji ciągłych zbioru ![]() w
w ![]() ).
).
![]() jest
liniowo zależny,
jest
liniowo zależny,
![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]()
![]() ,
,
![$u=\left[ \begin{array}{cc} 1 & 1 \\ 1 & 1
\end{array} \right] $](img374.gif) ,
,
![$v=\left[ \begin{array}{cc} 1 & 0 \\ 1 & 1 \end{array} \right]$](img375.gif)
![]() oraz
oraz ![]()
![]() ,
, ![]()
![]() i
i ![]() są skończenie wymiarowe, to
są skończenie wymiarowe, to
![]()
![]()
![]()
![]()
![]() oraz
oraz
![]() =
= ![]() +
+ ![]()
![]()
![]() .
.
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
, ![]()
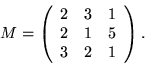
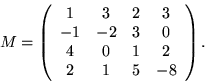
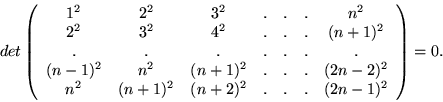
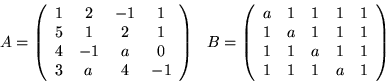
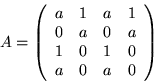
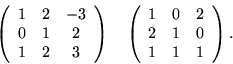
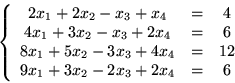
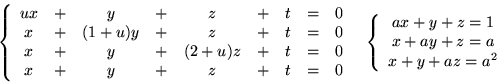
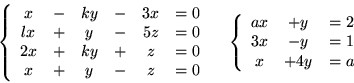
![]() jest bazą
jest bazą ![]() .
.
![]() względem tej
bazy.
względem tej
bazy.
![]() będzie operatorem liniowym
którego macierzą w bazie kanonicznej jest
będzie operatorem liniowym
którego macierzą w bazie kanonicznej jest
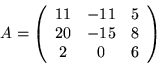
![]() w bazie
w bazie
![]() .
.
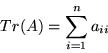
![]() i
i ![]() jeżeli
jeżeli
![]() zachodzi
zachodzi ![]() , gdzie
, gdzie ![]() jest
wielomianem charaktrystycznym macierzy
jest
wielomianem charaktrystycznym macierzy ![]() .
.
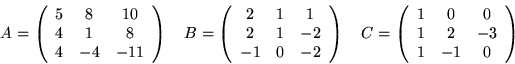
![]()
![]()
![]() w bazie kanonicznej.
w bazie kanonicznej.
![]() do postaci kanonicznej. Znajdź bazę
do postaci kanonicznej. Znajdź bazę
![]() w której
w której ![]() ma postać kanoniczną.
ma postać kanoniczną.
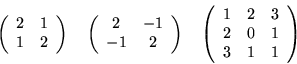
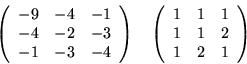
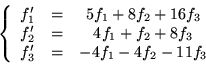
![]()
![]()
![]()
![]() i prostopadłej do wektora
i prostopadłej do wektora
![]()
![]() i równoległej do
wektorów
i równoległej do
wektorów ![]() i
i ![]() .
.