



Next: Całki powierzchniowe
Up: Zadania z matematyki dla
Previous: Algebra i geometria analityczna
Contents
- Ca
 kę
kę
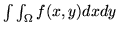 zamień na ca
zamień na ca ki
iterowane
ki
iterowane
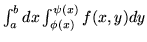
i
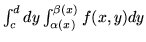 jesli
jesli 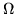 jest
jest
(a) trójkątem o wierzcho kach
kach 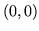 ,
, 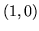 i
i 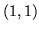
(b) ko em
em
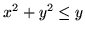 .
.
- Zmień kolejnosc ca
 kowania w ca
kowania w ca kach podwójnych :
kach podwójnych :
- Oblicz
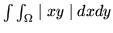 gdy
gdy 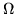 jest ko
jest ko em o srodku w
em o srodku w 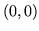 i
promieniu
i
promieniu 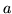 .
.
- Przechodząc do wspó
 rzędnych biegunowych oblicz
rzędnych biegunowych oblicz
- Narysuj bry
 ę której objętosc wyznacza ca
ę której objętosc wyznacza ca ka:
ka:
- Oblicz objętosci bry
 ograniczonych powierzchniami:
ograniczonych powierzchniami:
(a) 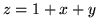 ,
, 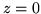 ,
, 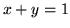 ,
, 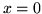 ,
, 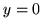 .
.
(b) 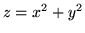 ,
, 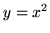 ,
, 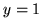 ,
, 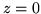 .
.
(c) 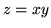 ,
, 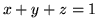 ,
, 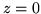 .
.
(d)
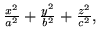
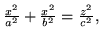
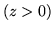 .
.
- Znajdź wspó
 rzędne srodka cięzkosci
jednorodnej figury ograniczonej krzywymi:
rzędne srodka cięzkosci
jednorodnej figury ograniczonej krzywymi:
- Oblicz pole które z powierzchni
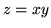 wycina walec
wycina walec 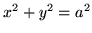 .
.
- Przy pomocy ca
 ki potrójnej oblicz objętosc bry
ki potrójnej oblicz objętosc bry y
ograniczonej powierzchniami:
y
ograniczonej powierzchniami:
- Przechodząc do wspó
 rzędnych cylindrycznych oblicz
rzędnych cylindrycznych oblicz
(gdzie 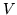 jest bry
jest bry ą
ograniczoną powierzchniami:
ą
ograniczoną powierzchniami: 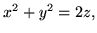
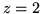 .
.
- Oblicz ca
 kę potrójną
kę potrójną
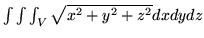 , gdzie
, gdzie 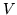 jest
bry
jest
bry ą ograniczoną powierzchnią
ą ograniczoną powierzchnią
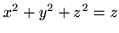 .
.
- Oblicz
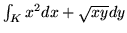 , gdzie
, gdzie 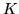 jest częscią
okręgu o srodku w
jest częscią
okręgu o srodku w 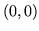 zawartym między punktami
zawartym między punktami 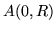 i
i 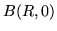 .
.
- Jaką pracę wykona punkt materialny poruszający się w polu
si
 :
:
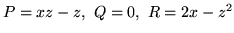 po
po  uku
uku 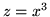
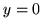 od
od 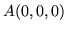 do
do
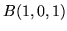 .
.
- Oblicz
(a)
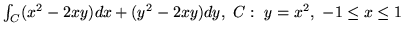
(b)
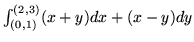
(c)
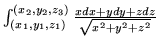
i korzystając z twierdzenia Greene'a
(d)
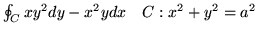 .
.
(e)
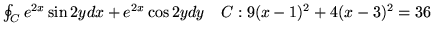
(f)
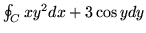 gdzie
gdzie 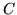 jest dodatnio zorientowanym brzegiem
obszaru ograniczonego krzywymi
jest dodatnio zorientowanym brzegiem
obszaru ograniczonego krzywymi 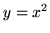 ,
, 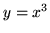 w pierwszej ćwiartce
układu współrzędnych.
w pierwszej ćwiartce
układu współrzędnych.
- Oblicz
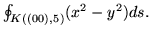
- Znajdź masę krzywej
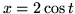 ,
, 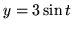 ,
, 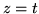 ,
,
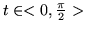 ,
której gęstość masy jest proporcjonalna do kwadratu odległości punktu od
punktu
,
której gęstość masy jest proporcjonalna do kwadratu odległości punktu od
punktu 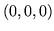 .
.
- Oblicz całki powierzchniowe niezorientowane:
- (a)
-
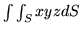 , gdzie
, gdzie  jest wycinkiem sfery
jest wycinkiem sfery
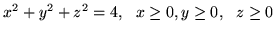 .
.
- (b)
-
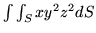 , gdzie
, gdzie  jest cęścią stożka
jest cęścią stożka
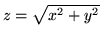 położoną nad podzbiorem płaszczyzny
położoną nad podzbiorem płaszczyzny 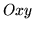 ograniczonym nierównościami:
ograniczonym nierównościami:
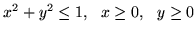 .
.
- (c)
-
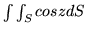 , gdzie
, gdzie  jest wycinkiem płaszczyzny
jest wycinkiem płaszczyzny
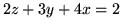 której rzutem na płaszczyzne
której rzutem na płaszczyzne 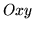 jest
jest
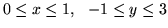 .
.
- (d)
-
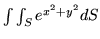 , gdzie
, gdzie  jet częścią stożka
jet częścią stożka
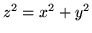 ponad kołem
ponad kołem
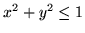 dla
dla 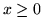 i
i 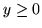 .
.
- (e)
-
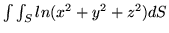 , gdzie
, gdzie  jest częścią sfery
jest częścią sfery
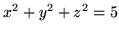 ponad kołem
ponad kołem
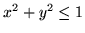 .
.
- (f)
-
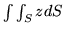 , gdzie
, gdzie  jest czworościanem ograniczonym
płaszczyznami układu współrzędnych i
jest czworościanem ograniczonym
płaszczyznami układu współrzędnych i 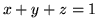 .
.
- (g)
-
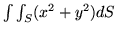 , gdzie
, gdzie  jest powierzchnią ograniczoną
zamkniętym walcem:
jest powierzchnią ograniczoną
zamkniętym walcem: 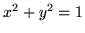 ,
,
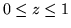 .
.
-
Oblicz strumień cieczy przepływającej ku górze przez
północną sferę
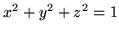 przy szybkości przepływu
przy szybkości przepływu
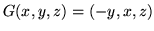 .
.
-
Oblicz całki powierzchniowe zorientowane:
- (a)
-
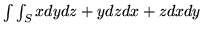 , gdy
, gdy
- (i)
 jest częścią płaszczyzny
jest częścią płaszczyzny
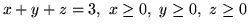 , zorientowaną ku górze
, zorientowaną ku górze
- (ii)
 jest zamkniętą, północną połową kuli:
jest zamkniętą, północną połową kuli:
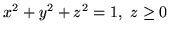 zorientowaną na zewnątrz.
zorientowaną na zewnątrz.
- (b)
-
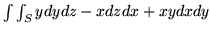 , gdy
, gdy  jest zadana przez:
jest zadana przez:
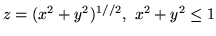
- Znajdź strumień wypływający na zewnątrz powierzchni zamkniętej
 gdy
gdy
- (a)
 jest czworościanem ograniczonym przez płaszczyznę
jest czworościanem ograniczonym przez płaszczyznę
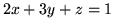 i płaszczyznami układu współrzędnych a prędkość
przepływu
i płaszczyznami układu współrzędnych a prędkość
przepływu
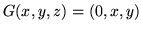 .
.
- (b)
 jest ograniczona przez stożek
jest ograniczona przez stożek
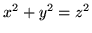 i płaszczyznę
i płaszczyznę 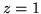
a prędkość przepływu
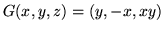 .
.
-
Podczas wykładu udowodniliśmy, że jeśli pole wektorowe
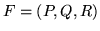 i powierzchnia
i powierzchnia  spełniają założenia twierdzenia
Gaussa-Ostrogradskiego, wtedy
spełniają założenia twierdzenia
Gaussa-Ostrogradskiego, wtedy
Udowodnij dwa "brakujące ogniwa" dowodu twierdzenia Gaussa-Ostrogradskiego,
t.j. równości
- Korzystając z twierdzenia Gaussa-Ostrogradzkiego oblicz te z całek zadań
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) i
i ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) w których
w których  jest powierzchnią zamkniętą.
jest powierzchnią zamkniętą.
- Oblicz strumień cieczy wypływający na zewnątrz powierzchni
 z
prędkością
z
prędkością 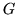 .
.
- (a)
-
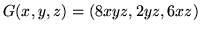 ,
,
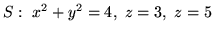
- (b)
-
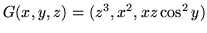 ,
, 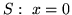 ,
,
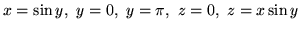 .
.
- (c)
-
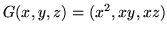 ,
,
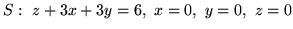 .
.
- (por.
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) )
Na wykładzie udowodniliśmy, że przy stosownych założeniach
(przypomnij jakich?!) o polu wektorowym
)
Na wykładzie udowodniliśmy, że przy stosownych założeniach
(przypomnij jakich?!) o polu wektorowym 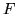 i powierzchni
i powierzchni  zachodzi
wzór
zachodzi
wzór
Udowodnij pozostałe dwa wzory uzupełniając w ten sposób dowód twierdzenia
Stokesa.
- Poniższe całki oblicz
- (a)
- korzystając ze wzoru na zamianę całki krzywoliniowej na oznaczoną (bez
korzystania z twierdzenia Stokesa),
- (b)
- korzystając z twierdzenia Stokesa.
(W każdym z przykładów wybierz jedną z dwóch możliwych orientacji
krzywej 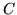 .)
.)
- (i)
-
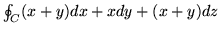 ,
,
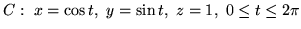
- (ii)
-
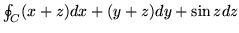 ,
,
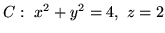
- Korzystając z twierdzenia Stokesa oblicz (
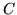 zorientuj jakkolwiek):
zorientuj jakkolwiek):
- (a)
-
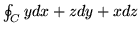 ,
, 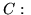 trójkąt o wierzchołkach
trójkąt o wierzchołkach
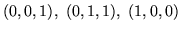 .
.
- (b)
-
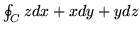 , gdzie
, gdzie 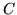 jest przecięciem powierzchni o równaniu
jest przecięciem powierzchni o równaniu
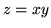 z walcem
z walcem 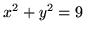 .
.
- (c)
-
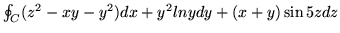 , gdzie
, gdzie 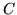 jest
przecięciem płaszczyzny
jest
przecięciem płaszczyzny 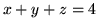 z płaszczyznami układu.
z płaszczyznami układu.




Next: Całki powierzchniowe
Up: Zadania z matematyki dla
Previous: Algebra i geometria analityczna
Contents
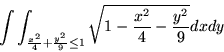
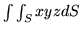 , gdzie
, gdzie  jest wycinkiem sfery
jest wycinkiem sfery
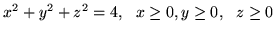 .
.
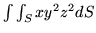 , gdzie
, gdzie  jest cęścią stożka
jest cęścią stożka
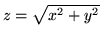 położoną nad podzbiorem płaszczyzny
położoną nad podzbiorem płaszczyzny 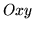 ograniczonym nierównościami:
ograniczonym nierównościami: 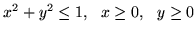 .
.
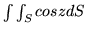 , gdzie
, gdzie  jest wycinkiem płaszczyzny
jest wycinkiem płaszczyzny
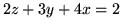 której rzutem na płaszczyzne
której rzutem na płaszczyzne 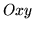 jest
jest
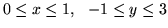 .
.
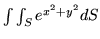 , gdzie
, gdzie  jet częścią stożka
jet częścią stożka
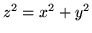 ponad kołem
ponad kołem 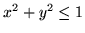 dla
dla 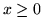 i
i 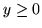 .
.
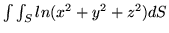 , gdzie
, gdzie  jest częścią sfery
jest częścią sfery
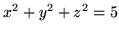 ponad kołem
ponad kołem
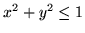 .
.
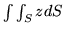 , gdzie
, gdzie  jest czworościanem ograniczonym
płaszczyznami układu współrzędnych i
jest czworościanem ograniczonym
płaszczyznami układu współrzędnych i 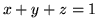 .
.
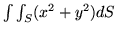 , gdzie
, gdzie  jest powierzchnią ograniczoną
zamkniętym walcem:
jest powierzchnią ograniczoną
zamkniętym walcem: 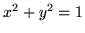 ,
,
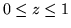 .
.
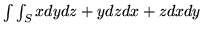 , gdy
, gdy
 jest częścią płaszczyzny
jest częścią płaszczyzny
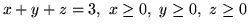 , zorientowaną ku górze
, zorientowaną ku górze
 jest zamkniętą, północną połową kuli:
jest zamkniętą, północną połową kuli:
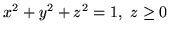 zorientowaną na zewnątrz.
zorientowaną na zewnątrz.
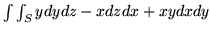 , gdy
, gdy  jest zadana przez:
jest zadana przez:
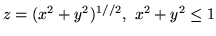
 jest czworościanem ograniczonym przez płaszczyznę
jest czworościanem ograniczonym przez płaszczyznę
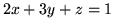 i płaszczyznami układu współrzędnych a prędkość
przepływu
i płaszczyznami układu współrzędnych a prędkość
przepływu
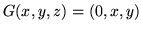 .
.
 jest ograniczona przez stożek
jest ograniczona przez stożek
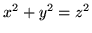 i płaszczyznę
i płaszczyznę 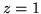
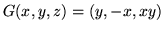 .
.
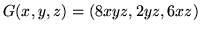 ,
,
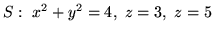
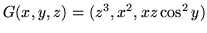 ,
, 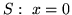 ,
,
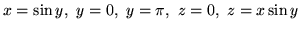 .
.
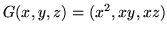 ,
,
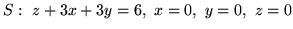 .
.
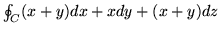 ,
,
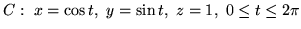
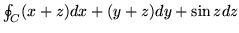 ,
,
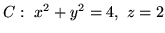
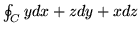 ,
, 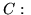 trójkąt o wierzchołkach
trójkąt o wierzchołkach
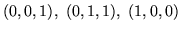 .
.
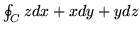 , gdzie
, gdzie 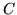 jest przecięciem powierzchni o równaniu
jest przecięciem powierzchni o równaniu
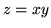 z walcem
z walcem 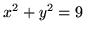 .
.
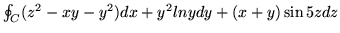 , gdzie
, gdzie 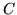 jest
przecięciem płaszczyzny
jest
przecięciem płaszczyzny 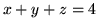 z płaszczyznami układu.
z płaszczyznami układu.