


Next: Klasa funkcji cylindrycznych
Up: Problem Sturma-Liouville'a na
Previous: Funkcje Bessel'a
Niech
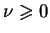 ; rozważny taki problem brzegowy na wartości
własne:
; rozważny taki problem brzegowy na wartości
własne:
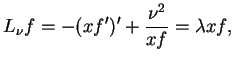 |
(13.31) |
gdzie
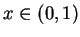 , oraz dla
, oraz dla
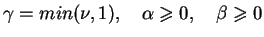 i
i
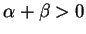
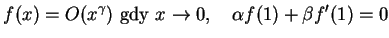 |
(13.32) |
Dziedzina
![% latex2html id marker 23611
$ Dom(L_{\nu})=C^{2}\big([0,1] \big) \oplus
(\ref{sec:13.31})$](img1635.gif) oraz warunek, że
oraz warunek, że
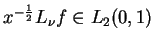 dla
dla
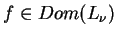 . Oczywiście, że operator
. Oczywiście, że operator 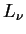 jest dodatni,
hermitowy i zachodzi równość:
jest dodatni,
hermitowy i zachodzi równość:
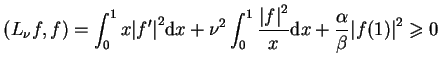 |
(13.33) |
dla
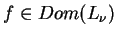 .
.
Niech teraz 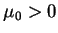 jest pierwiastkiem równania
jest pierwiastkiem równania
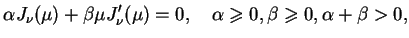 |
(13.34) |
gdzie
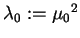 jest wartością własną, a
jest wartością własną, a
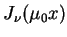 jest odpowiednią funkcją własną. Przy tym
znajdujemy, że
jest odpowiednią funkcją własną. Przy tym
znajdujemy, że
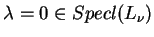 tylko wtedy gdy
tylko wtedy gdy
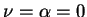 , co przeczy warunkowi
, co przeczy warunkowi
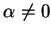 . Tak
więc dla rozwiązania
. Tak
więc dla rozwiązania
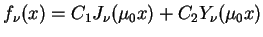 |
(13.35) |
zachodzi z pierwszego warunku (13.32), że 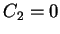 ,
oraz wartość
,
oraz wartość
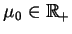 spełnia równanie
(13.34). Wnioskując z (13.35) i
(13.34), otrzymujemy że
spełnia równanie
(13.34). Wnioskując z (13.35) i
(13.34), otrzymujemy że
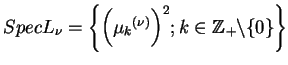 i
i
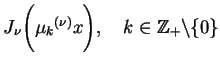 są odpowiednio funkcje własne
operatora Bessel'a (13.31). Oczywiście także, że
zmodyfikowane że własne funkcje Bessel'a są ortogonalne na
są odpowiednio funkcje własne
operatora Bessel'a (13.31). Oczywiście także, że
zmodyfikowane że własne funkcje Bessel'a są ortogonalne na
![$ [0,1]$](img1596.gif) i gęste w
i gęste w
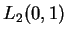 , tj. funkcje
, tj. funkcje
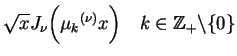 są gęste w
są gęste w
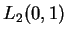 i
ortogonalne na
i
ortogonalne na ![$ (0,1]$](img1653.gif) . To jest równoważne temu, że zbiór
funkcji
. To jest równoważne temu, że zbiór
funkcji
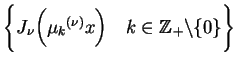 jest gęsty w
jest gęsty w
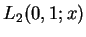 , przestrzeni Hilberta z funkcją wagową
, przestrzeni Hilberta z funkcją wagową 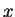 na
odcinku
na
odcinku 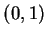 .
.



Next: Klasa funkcji cylindrycznych
Up: Problem Sturma-Liouville'a na
Previous: Funkcje Bessel'a
Andrzej Janus Szef
2001-12-05
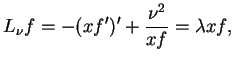
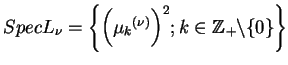 i
i
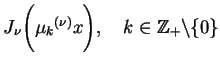 są odpowiednio funkcje własne
operatora Bessel'a (13.31). Oczywiście także, że
zmodyfikowane że własne funkcje Bessel'a są ortogonalne na
są odpowiednio funkcje własne
operatora Bessel'a (13.31). Oczywiście także, że
zmodyfikowane że własne funkcje Bessel'a są ortogonalne na
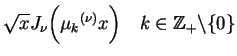 są gęste w
są gęste w
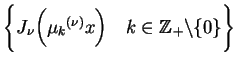 jest gęsty w
jest gęsty w