| (3.1) |
Oczywiście, że
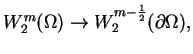 gdzie przestrzeń
gdzie przestrzeń
Teraz , niech
![]()
![]() jest ciągiem aproksymującym element
jest ciągiem aproksymującym element
![]()
![]() gdy
gdy
![]() Na mocy twierdzenia
(3.2) ciąg
Na mocy twierdzenia
(3.2) ciąg
![]()
![]() jest zbieżny w sensie
jest zbieżny w sensie
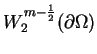 do pewnej funkcji
do pewnej funkcji
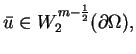 nie
zależnej od wyboru ciągu
nie
zależnej od wyboru ciągu
![]()
![]() Kładziemy wówczas
Kładziemy wówczas
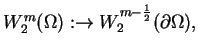 i jest oprócz tego
jeszcze surjektywnym (tj. ,,na''): dla każdego elementu
i jest oprócz tego
jeszcze surjektywnym (tj. ,,na''): dla każdego elementu
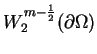 istnieje
taki element
istnieje
taki element 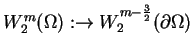 i posiada własności
podobne do twierdzenia (3.2), gdzie
i posiada własności
podobne do twierdzenia (3.2), gdzie 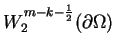 . Tak więc odwzorowanie
. Tak więc odwzorowanie