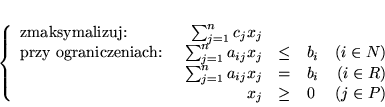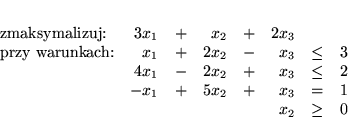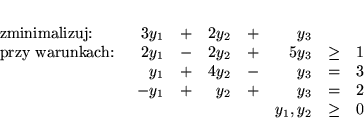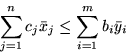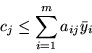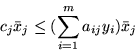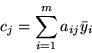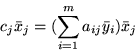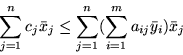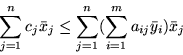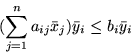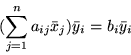Next: Ćwiczenia
Up: Dualizm
Previous: Interpretacja ekonomiczna
Spis rzeczy
Indeks
Dualność ogólniej
Jak zobaczymy w ustępie ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) , czasami wygodnie będzie nam dysponowąć
problemem dualnym do PPL w następującej postaci:
, czasami wygodnie będzie nam dysponowąć
problemem dualnym do PPL w następującej postaci:
|
(4.17) |
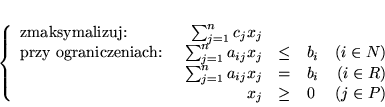 |
W PPL postaci (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) tylko o części zmiennych
) tylko o części zmiennych 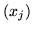 zakładamy,
że są nieujemne (dla
zakładamy,
że są nieujemne (dla 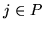 ), pozostałe zmienne nazywamy wolnymi,
a zbiór indeksów zmiennych wolnych oznaczamy przez
), pozostałe zmienne nazywamy wolnymi,
a zbiór indeksów zmiennych wolnych oznaczamy przez
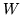 4.3
4.3
Definicja 4.2
Problemem dualnym do (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
) nazywamy problem programowania liniowego
następującej postaci:
|
(4.18) |
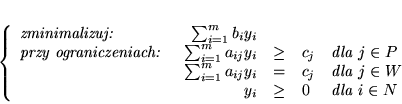 |
Problem (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
) nazywamy wtedy
problemem prymalnym (względem (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
)).
Przykład 4.3
Problemem dualnym do PPL
jest PPL
Rzeczywiście, w naszym przykładzie mamy
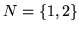
,
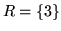
,
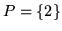
,
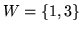
.

Wyniki jakie otrzymamy dla problemów (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) i (
) i (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) są uogólnieniami
twierdzeń ustępu
) są uogólnieniami
twierdzeń ustępu ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) w tym sensie, że jeśli w problemach
(
w tym sensie, że jeśli w problemach
(![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) i (
) i (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) położymy
) położymy 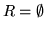 i
i 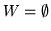 (a więc
(a więc
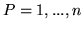 ), to poniższe twierdzenia
), to poniższe twierdzenia ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) i
i ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) sprowadzają się do twierdzeń
sprowadzają się do twierdzeń ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) i
i ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) .
.
Twierdzenie 4.8
Jeżeli
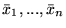
i
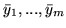
są
rozwiązaniami dopuszczalnymi problemów, odpowiednio (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
) i (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
),
to zachodzi nierówność
Dowód twierdzenia ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) niewiele różni się od dowodu twierdzenia
niewiele różni się od dowodu twierdzenia ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) .
.
Dla 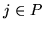 mamy
mamy
co po wymnożeniu przez 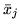 (pamiętamy, że wtedy
(pamiętamy, że wtedy
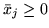 ) daje
) daje
Z kolei dla 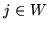
i wobec tego
Sumując te wzory po wszystkich 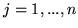 otrzymamy
otrzymamy
co po łatwych przekształceniach daje
Dla 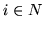 mamy
mamy
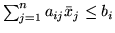 oraz
oraz
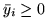 , więc
, więc
Podobnie, dla 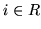
Znowu sumując po
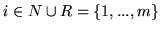 otrzymamy ostatecznie
otrzymamy ostatecznie
i dowód twierdzenia ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) jest zakończony.
Czytelnika który nie jest jeszcze znużony kolejnym wykorzystaniem metody
sympleksowej którą poznał w rozdziale 3, zachęcamy do samodzielnego
udowodnienia przedstawionej poniżej uogólnionej zasady dualności (lub do
odszukania dowodu w literaturze (np. w [4]).
jest zakończony.
Czytelnika który nie jest jeszcze znużony kolejnym wykorzystaniem metody
sympleksowej którą poznał w rozdziale 3, zachęcamy do samodzielnego
udowodnienia przedstawionej poniżej uogólnionej zasady dualności (lub do
odszukania dowodu w literaturze (np. w [4]).
Twierdzenie 4.9
[Ogólna zasada dualności]
Jeżeli problem prymalny (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
) ma rozwiązanie optymalne,
to także problem dualny (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
) ma rozwiązanie optymalne i wartości funkcji
celu obu tych rozwiązań są równe.
Uwaga. Łatwo zauważyć, że jeśli wymnożymy w obu problemach
(![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) i (
) i (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) )
funkcje celu oraz
nierówności w pierwszych linijkach ograniczeń
przez
)
funkcje celu oraz
nierówności w pierwszych linijkach ograniczeń
przez 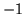 , to otrzymamy sytuację w której problem (
, to otrzymamy sytuację w której problem (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) jest problemem
w którym maksymalizujemy funkcję celu i problemem do niego dualnym jest (
) jest problemem
w którym maksymalizujemy funkcję celu i problemem do niego dualnym jest (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ).
Stąd prawdziwy jest wniosek:
).
Stąd prawdziwy jest wniosek:
Wniosek 4.10
Jeśli (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
) ma rozwiązanie optymalne, to także (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
)
ma rozwiązanie
optymalne i wartości tych rozwiązań są identyczne.





Next: Ćwiczenia
Up: Dualizm
Previous: Interpretacja ekonomiczna
Spis rzeczy
Indeks