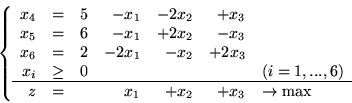Ćwiczenie 5.2
Wykaż, że jeśli zbiór wierszy macierzy
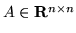
można podzielić na dwa
rozłączne podzbiory
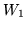
i
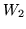
takie, że dla każdego
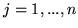
spełniona jest równość
(
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
), to
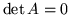
(prawdziwe także gdy jeden ze zbiorów
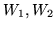
jest
pusty
5.3).
Ćwiczenie 5.3
Niech będą dane macierz totalnie unimodularna
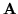
,
układ nierówności
|
(5.21) |
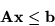 |
oraz mu układ
|
(5.22) |
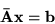 |
powstały z (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
) przez wprowadzenie
zmiennych dodatkowych. Wykaż, żemacierz
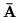
jest totalnie unimodularna.
Ćwiczenie 5.4
Z twierdzenia
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
nie wynika, że jeśli są spełnionezałożenia
tego twierdzenia, to
wszystkie rozwiązania problemu(
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
) są całkowite.
Skonstruuj przykład PPL w którym macierzograniczeń
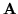
jest totalnie unimodularnai wektor
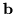
całkowity, dla
którego istnieją optymalne rozwiązania niecałkowite.
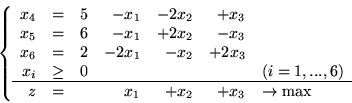
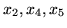 są zmiennymi bazowymi pewnego słownika.
są zmiennymi bazowymi pewnego słownika.