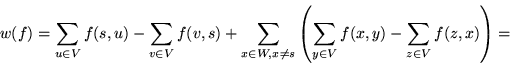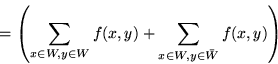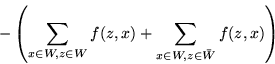Next: Maksymalny przepływ a dualność
Up: Metody sieciowe
Previous: Sieci
Spis rzeczy
Indeks
W sieci 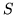 może być wyróżniony pewien wierzchołek
może być wyróżniony pewien wierzchołek 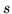 , nazywany źródłem
i inny
wierzchołek, powiedzmy
, nazywany źródłem
i inny
wierzchołek, powiedzmy 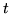 , który nazywać będziemy odpływem.
, który nazywać będziemy odpływem.
Niech 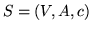 będzie siecią o źródla
będzie siecią o źródla 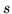 i odpływie
i odpływie 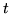 oraz nieujemnej funkcji przepustowości
oraz nieujemnej funkcji przepustowości 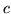 . O nieujemnej funkcji
. O nieujemnej funkcji
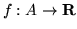 mówimy, że jest
przepływem z
mówimy, że jest
przepływem z 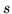 do
do 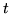 w
w 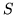 jeżeli spełnia następujące
warunki:
jeżeli spełnia następujące
warunki:
|
(8.2) |
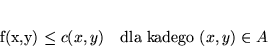 |
|
(8.3) |
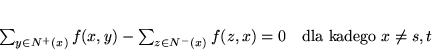 |
Liczbę
nazywamy wartością przepływu 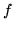 .
.
Przykład 8.2
Niech
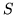
będzie siecią jak na rysunku 8.3. Liczby wypisane obok łuków w kwadracikach
oznaczają przepustowości łuków, a te bez kwadracików przepływy. Jest bardzo łatwym
sprawdzenie, że na rysunku poprawnie zdefiniowany jest przepływ (spełnia warunki
(
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
) i (
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
)), a wartoć tego przepływu wynosi
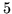
.

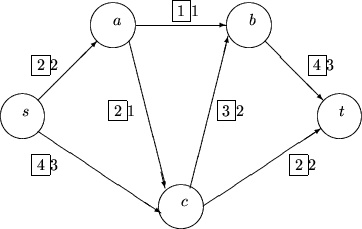
Rys. 8.3
Problem optymalizacyjny narzuca się teraz sam.
Problem maksymalnego przepływu.
Dla danej sieci 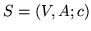 o źródle
o źródle 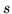 i odpływie
i odpływie 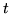 znaleźć przepływ
o maksymalnej wartości.
znaleźć przepływ
o maksymalnej wartości.
W dalszym ciągu będzie nam wygodnie będzie nam przyjąć zamiast
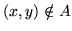 ,
,
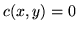 i istnienie wszystkich możliwych łuków w sieci. Interpretacja takiej umowy jest oczywista: nie ma przepływu (a raczej jest przepływ zerowy) na nieistniejących łukach8.6.
Wtedy warunki (
i istnienie wszystkich możliwych łuków w sieci. Interpretacja takiej umowy jest oczywista: nie ma przepływu (a raczej jest przepływ zerowy) na nieistniejących łukach8.6.
Wtedy warunki (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) i (
) i (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) można zapisać, odpowiednio,
) można zapisać, odpowiednio,
|
(8.4) |
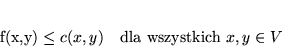 |
|
(8.5) |
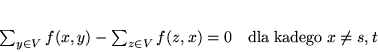 |
a wzór na wartość przepływu
|
(8.6) |
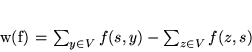 |
Zauważmy, że przepływ w przykładzie ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) nie jest maksymalny. Zwiększając przepływ na łukach:
nie jest maksymalny. Zwiększając przepływ na łukach:
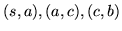 i
i 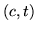 o
o  otrzymamy przepływ (warunki (
otrzymamy przepływ (warunki (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) i (
) i (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) są dalej spełnione)
i wartość tego
przepływu wynosi
) są dalej spełnione)
i wartość tego
przepływu wynosi 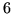 . Okaże się, że ten prosty pomysł znajdowania ścieżki prowadzącej
z
. Okaże się, że ten prosty pomysł znajdowania ścieżki prowadzącej
z 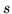 do
do 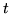 wzdłóż której można zwiększyć przepływ na poszczególnych łukach
o stałą wartość, jest kluczową ideą prowadzącą do rozwiązania problemu maksymalnego
przepływu w sieciach.
wzdłóż której można zwiększyć przepływ na poszczególnych łukach
o stałą wartość, jest kluczową ideą prowadzącą do rozwiązania problemu maksymalnego
przepływu w sieciach.
Jest najzupełniej oczywiste, że problem maksymalnego przepływu jest
problemem programowania
liniowego. Wierzchołki sieci nazwiemy
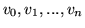 , z
, z 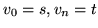 , a przepływ
na łuku
, a przepływ
na łuku 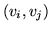 oznaczymy przez
oznaczymy przez 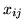 (zamiast
(zamiast 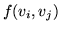 a
przepustowość łuku
a
przepustowość łuku 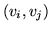 przez
przez 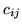 . Nasz problem maksymalnego przepływu jest PPL:
. Nasz problem maksymalnego przepływu jest PPL:
|
(8.7) |
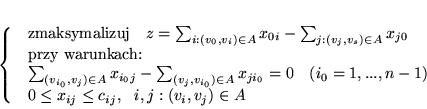 |
Zauważmy, że jeśli zbiór wierzchołków sieci jest skończony (a tylko takie sieci
tu rozważamy) a przepustowości łuków są liczbami skończonymi, to problem
(![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) jest ograniczony, posiada więc rozwiązanie optymalne.
Z powyższego oraz twierdzenia
) jest ograniczony, posiada więc rozwiązanie optymalne.
Z powyższego oraz twierdzenia ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) wynika następujący wniosek.
wynika następujący wniosek.
Wniosek 8.2
Jeśli funkcja przepustowości łuków przyjmuje wartości całkowite, to problem
maksymalnego przepływu w tej sieci ma całkowite rozwiązanie optymalne.
Ważnym pojęciem dla problemu maksymalnego przepływu są przekrój i jego wartość.
Niech będzie dana sieć 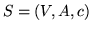 ze źródłem
ze źródłem 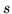 i odpływem
i odpływem 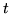 i niech
i niech 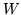 będzie
takim podzbiorem
będzie
takim podzbiorem 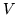 , że
, że 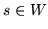 i
i 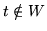 . Zbiór
. Zbiór 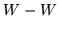 oznaczmy przeż
oznaczmy przeż 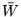 .
Zbiór łuków
.
Zbiór łuków
nazywamy przekrojem rozdzielającym 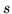 od
od 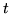 lub krótko przekrojem. Liczbę
lub krótko przekrojem. Liczbę
nazywamy przepustowością przekroju
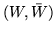 .
.
Twierdzenie 8.3
Niech
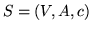
będzie siecią o źródle
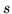
i odpływie
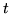
. Dla dowolnego przepływu
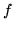
i dla dowolnego przekroju
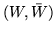
zachodzi nierówność
Dowód. Sumując odpowiednio wzory (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) i (
) i (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) po wszystkich
) po wszystkich 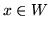 i pamiętając, że
i pamiętając, że
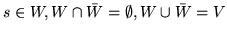 , otrzymamy
, otrzymamy
Zauważmy, że
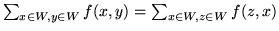 ,
a wobec tego
,
a wobec tego
|
(8.8) |
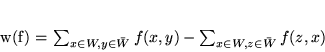 |
Wartości 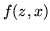 są nieujemne, uwzględniając więc nierówności (
są nieujemne, uwzględniając więc nierówności (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) )
otrzymujemy
)
otrzymujemy
|
(8.9) |
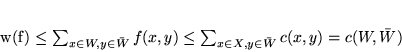 |
co kończy dowód.
Uwaga 8.1
Jeżeli uda nam się znaleźć przepływ
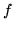
i przekrój
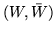
takie, że
to na mocy twierdzenia
![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif)
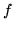
jest przepływem maksymalnym (a przekrój
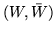
ma minimalną przepustowość).
Niejako po drodze w dowodzie twierdzenia ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) otrzymaliśmy ważną
równość (
otrzymaliśmy ważną
równość (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) którą teraz zapiszemy nieco inaczej.
) którą teraz zapiszemy nieco inaczej.
Uwaga 8.2
Dla każdego przepływu
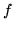
i przekroju
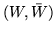
zachodzi wzór
|
(8.10) |
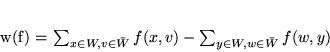 |
Wniosek ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) oznacza, że w przyrodzie nic nie ginie, to co
wypłynęło ze źródła wpływa do odpływu!
oznacza, że w przyrodzie nic nie ginie, to co
wypłynęło ze źródła wpływa do odpływu!
Dowód wniosku ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) .
Wystarczy zastosować wzór (
.
Wystarczy zastosować wzór (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) do
) do
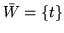 .
Twierdzenie
.
Twierdzenie ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) da nam możliwość udowodnienia twierdzenia o
maksymalnym przepływie i minimalnym przekroju, odkrytego niezależnie przez Forda i
Fulkersona [8] oraz Eliasa, Feinsteina i Shannona [7].
da nam możliwość udowodnienia twierdzenia o
maksymalnym przepływie i minimalnym przekroju, odkrytego niezależnie przez Forda i
Fulkersona [8] oraz Eliasa, Feinsteina i Shannona [7].
Twierdzenie 8.5 (Max flow min cut theorem)
Maksymalna wartość
przepływu
ze źródła
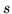
do odpływu
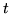
w sieci jest równa wartości minimalnego przekroju
rozdzielającego
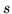
od
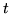
:
Dowód twierdzenia ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) polega de facto na wskazaniu algorytmu
pozwalającego znależć maksymalny przepływ w sieci, tzw.
algorytm ścieżki powiększającej
Forda-Fulkersona (p. [9]). Formalnie algorytm ten zostanie przedstawiony później.
polega de facto na wskazaniu algorytmu
pozwalającego znależć maksymalny przepływ w sieci, tzw.
algorytm ścieżki powiększającej
Forda-Fulkersona (p. [9]). Formalnie algorytm ten zostanie przedstawiony później.
Niech 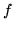 będzie przepływem maksymalnym w sieci
będzie przepływem maksymalnym w sieci 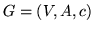 ze źródła
ze źródła 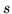 do
odpływu
do
odpływu 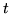 . Utwórzmy rekurencjnie zbiór
. Utwórzmy rekurencjnie zbiór 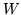 w następujący sposób:
w następujący sposób:
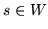
- jeśli
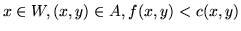 to
to 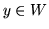
- jeśli
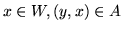 i
i 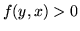 to
to 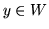 .
.
Kluczową ideą dowodu jest obserwacja, że dla każdego wierzchołka 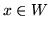 istnieje ścieżka
istnieje ścieżka
taka, że
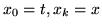 i dla każdego
i dla każdego 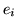 zachodzi albo
zachodzi albo
|
(8.11) |
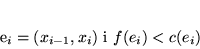 |
albo
|
(8.12) |
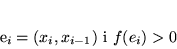 |
Inaczej mówiąc: wartość przepływu jest mniejsza od przepustowości na wszystkich łukach zgodnych i dodatnia na niezgodnych łukach ścieżki 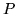 .
.
Gdyby 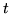 należało do
należało do 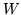 , to istniałaby ścieżka
, to istniałaby ścieżka 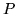 z
z 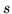 do
do 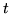 (tj. taka, że
(tj. taka, że
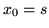 i
i 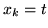 ) spełniająca warunki (
) spełniająca warunki (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) )-(
)-(![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ). Niech
). Niech
oraz
Jest oczywistym, że
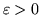 , i że dodając
, i że dodając 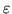 do funkcji przepływu na łukach ścieżki
do funkcji przepływu na łukach ścieżki 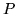 zgodnych i odejmując
zgodnych i odejmując 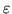 na łukach ścieżki
na łukach ścieżki 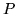 niezgodnych, inaczej mówiąc: definiując funkcję
niezgodnych, inaczej mówiąc: definiując funkcję
otrzymalibyśmy nową funkcję przepływu której wartość wynosiłaby
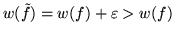 co byłoby sprzeczne z maksymalnościa przepływu
co byłoby sprzeczne z maksymalnościa przepływu 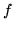 .
.
Stąd wynika, że 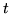 nie jest elementem zbioru
nie jest elementem zbioru 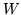 i zbiór
i zbiór 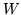 ma następujące własności:
ma następujące własności:
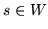
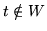
- jeśli
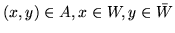 to
to 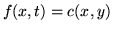
- jeśli
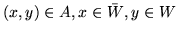 to
to 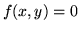
Wobec (1) i (2) 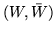 jest przekrojem rozdzielającym
jest przekrojem rozdzielającym 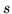 i
i 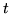 .
Łuki spełniające (3) nazywają sie nasyconymi
, a takie które spełniają (4)
wyschniętymi.
Wobec (3) i (4) mamy
.
Łuki spełniające (3) nazywają sie nasyconymi
, a takie które spełniają (4)
wyschniętymi.
Wobec (3) i (4) mamy
co wobec twierdzenia ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) dowodzi, że
dowodzi, że 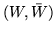 jest przekrojem o przepustowości minimalnej.
jest przekrojem o przepustowości minimalnej.





Next: Maksymalny przepływ a dualność
Up: Metody sieciowe
Previous: Sieci
Spis rzeczy
Indeks