Next: Algorytm Forda-Fulkersona
Up: Metody sieciowe
Previous: Przepływy w sieciach
Spis rzeczy
Indeks
W tym podrozdziale okaże się, że twierdzenie o maksymalnym przepływie
i minimalnym przekroju jest - w pewien sposób -
zasadą dualności dla problemu maksymalnego przepływu.
Zapiszmy problem maksymalnego przepływu (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) - (
) - (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) w nieco innej postaci.
Niech będzie dana sieć
) w nieco innej postaci.
Niech będzie dana sieć 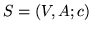 . Przepływem w
. Przepływem w  jest funkcja
jest funkcja
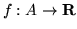 spełniająca następujące warunki:
spełniająca następujące warunki:
|
(8.13) |
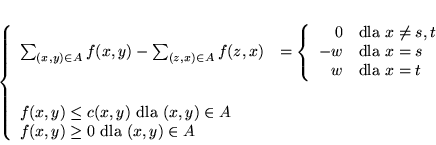 |
Wartością przepływu 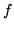 jest wtedy liczba
jest wtedy liczba 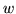 którą w naszym
problemie maksymalizujemy:
którą w naszym
problemie maksymalizujemy:
|
(8.14) |
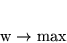 |
Problemem dualnym do problemu (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) - (
) - (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) jest problem
następujący (por. podrozdział
) jest problem
następujący (por. podrozdział ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ):
):
|
(8.15) |
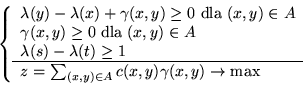 |
Zauważmy, że w problemie dualnym (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) nie ma ograniczeń na znak zmiennych
dualnych
) nie ma ograniczeń na znak zmiennych
dualnych 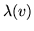 (dla
(dla 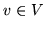 ). Zmienne dualne odpowiadają poszczegłnym
ograniczeniom w problemie prymalnym. Tak więc
). Zmienne dualne odpowiadają poszczegłnym
ograniczeniom w problemie prymalnym. Tak więc
-
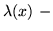
- są zmiennymi odpowiadającymi ograniczeniom
|
(8.16) |
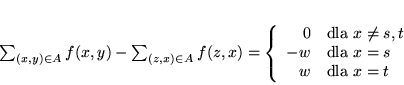 |
Każdemu wierzchołkowi 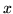 sieci
sieci  odpowiada zmienna dualna która nie ma
ograniczenia na znak gdyż we wzorze (
odpowiada zmienna dualna która nie ma
ograniczenia na znak gdyż we wzorze (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) jest równość.
) jest równość.
-
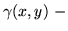
- są zmiennymi dualnymi odpowiadającymi ograniczeniu
|
(8.17) |
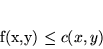 |
stąd w problemie dualnym występuje ograniczenie na znak tej zmiennej8.7.
Dowolny przekrój
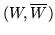 rozdzielający
rozdzielający 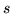 od
od 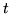 w sieci
w sieci  definiuje
pewne rozwiązanie dopuszczalne problemu (
definiuje
pewne rozwiązanie dopuszczalne problemu (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) w następujący sposób:
) w następujący sposób:
|
(8.18) |
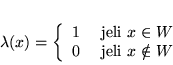 |
|
(8.19) |
 |
Słaba zasada dualności w ogólnej postaci (twierdzenie ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) daje nam natychmiast
inny dowód twierdzenia
) daje nam natychmiast
inny dowód twierdzenia ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) . Rzeczywiście, funkcje
. Rzeczywiście, funkcje 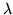 i
i 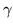 zdefiniowane
wzorami (
zdefiniowane
wzorami (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) i (
) i (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) przez dowolny przekrój rozdzielający
) przez dowolny przekrój rozdzielający 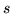 od
od 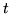 dają pewne
rozwiązanie problemu (
dają pewne
rozwiązanie problemu (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ).
).
Z kolei cała reszta dowodu twierdzenia ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) sprowadza się do wykazania, że pewien
przekrój określa nam przy pomocy (
sprowadza się do wykazania, że pewien
przekrój określa nam przy pomocy (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) i (
) i (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) ) rozwiązanie optymalne (
) rozwiązanie optymalne (![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) )
(zrobili to Dantzig i Fulkerson w [6]).
)
(zrobili to Dantzig i Fulkerson w [6]).





Next: Algorytm Forda-Fulkersona
Up: Metody sieciowe
Previous: Przepływy w sieciach
Spis rzeczy
Indeks