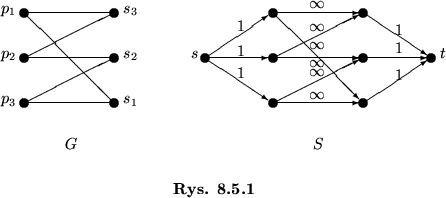
Przykład 8.4
W pewnym zakładzie pracy zatrudnieni są pracownicy
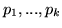
.
W zakładzie tym są też
stanowiska pracy
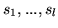
, przy czym nie każdy pracownik może pracować przy każdym
stanowisku. Dla dobrego funkcjonowania zakładu istotny jest problem jak przydzielić
stanowiska pracy wszystkim zatrudnionym, by optymalnie wykorzystać pracowników
i obsadzić stanowiska pracy.
Taka sytuacja łatwo daje się opisać przy pomocy grafu dwudzielnego
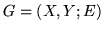
,
gdzie
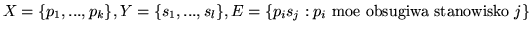
.
Nasz problem w języku teorii grafów można sformułować tak:
znajdź w 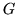 skojarzenie
skojarzenie
 o
maksymalnej liczbie krawędzi
o
maksymalnej liczbie krawędzi. Sytuacja będzie oczywiście najlepsza wtedy, gdy takie
skojarzenie będzie
pełnym skojarzeniem 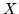 w
w 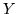
grafu dwudzielnego
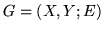
, t.j. wtedy gdy dla każdego
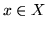
istnieje krawędź
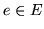
taka, że
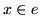 8.12
8.12.
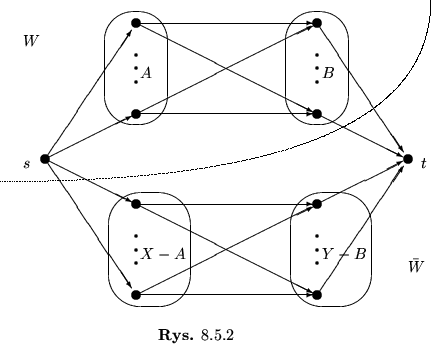
Twierdzenie 8.7 (P. Hall)
Niech
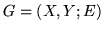
będzie grafem dwudzielnym. W
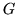
istnieje skojarzenie pełne
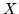
w
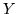
wtedy i tylko wtedy, jeśli dla każdego podzbioru
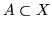
zachodzi
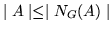
.