




Next: Przepływ całkowity. Zbieżność Algorytmu
Up: Metody sieciowe
Previous: Maksymalny przepływ a dualność
Spis rzeczy
Indeks
Niech 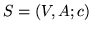 będzie siecią a
będzie siecią a 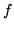 przepływem w
przepływem w  - jeśli nie mamy
lepszego, może to być przepływ zerowy,
tj. przepływ równy zero na wszystkich łukach sieci.
Algorytm - wykorzystujący ideę dowodu twierdzenia
- jeśli nie mamy
lepszego, może to być przepływ zerowy,
tj. przepływ równy zero na wszystkich łukach sieci.
Algorytm - wykorzystujący ideę dowodu twierdzenia ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) polega na cechowaniu wierzchołków sieci cechami postaci
polega na cechowaniu wierzchołków sieci cechami postaci
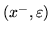 lub
lub
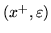 oraz modyfikacji
przepływu jeśli
oraz modyfikacji
przepływu jeśli 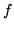 okazał się przepływem który nie jest
maksymalny lub znalezieniu przekroju o przepustowości równej
wartości przepływu
okazał się przepływem który nie jest
maksymalny lub znalezieniu przekroju o przepustowości równej
wartości przepływu 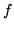 .
.
Cechowanie. Wierzchołkowi 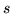 nadajemy cechę
nadajemy cechę 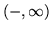 .
.
Niech 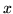 będzie wierzchołkiem ocechowanym. Z wierzchołka
będzie wierzchołkiem ocechowanym. Z wierzchołka 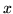 cechujemy nieocechowane jeszcze wierzchołki w jednej z dwóch sytuacji:
cechujemy nieocechowane jeszcze wierzchołki w jednej z dwóch sytuacji:
- (a)
- jeśli istnieje wierzchołek nieocechowany
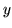 taki, że
taki, że
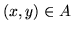 i
i
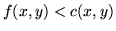 to wierzchołkowi
to wierzchołkowi
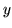 nadajemy cechę
nadajemy cechę
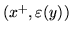 , gdzie
, gdzie
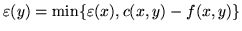 ,
,
- (b)
- jeśli istnieje nieocechowany wierzchołek
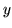 taki,
że
taki,
że 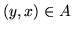 i
i 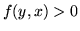 to wierzchołkowi
to wierzchołkowi 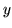 nadajemy cechę
nadajemy cechę
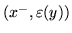 , gdzie
, gdzie
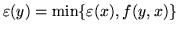
Postępowanie cechowania kończy się jeżeli został
ocechowany odpływ 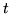 lub nie ocechowano
lub nie ocechowano 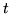 lecz
procesu cechowania nie da się kontynuować
(żadnego jeszcze nieocechowanego wierzchołka nie
da się już ocechować).
lecz
procesu cechowania nie da się kontynuować
(żadnego jeszcze nieocechowanego wierzchołka nie
da się już ocechować).
- (i)
- Jeżeli ocechowaliśmy wierzchołek
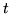 to
to 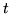 otrzymał
cechę postaci
otrzymał
cechę postaci
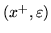 lub
lub
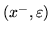 (dla pewnego
(dla pewnego 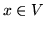 ).
).
W pierwszym przypadku modyfikujemy przepływ na łuku
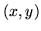 wzorem
wzorem
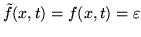 , w drugim
, w drugim
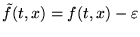 .
.
Wierzchołek 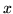 jest ocechowany. Jeżeli pierwszy element jego
cechy jest postaci
jest ocechowany. Jeżeli pierwszy element jego
cechy jest postaci 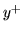 to do przepływu na łuku
to do przepływu na łuku 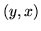 dodajemy
dodajemy 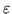 , jeżeli jest to
, jeżeli jest to 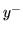 od przepływu
na łuku
od przepływu
na łuku 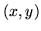 odejmujemy
odejmujemy 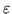 .
.
Powtarzając tę czynność odpowiednią liczbę razy dojdziemy
w końcu do źródła 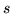 . Dojdziemy wzdłóż wskazanej
przez pierwsze elementy cech wierzchołków ścieżkę zwaną
ścieżką powiększającą
8.8. Oczywiście wartość nowego przepływu
. Dojdziemy wzdłóż wskazanej
przez pierwsze elementy cech wierzchołków ścieżkę zwaną
ścieżką powiększającą
8.8. Oczywiście wartość nowego przepływu
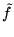 wynosi
wynosi
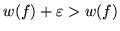 . Proces cechowania
rozpoczynamy od nowa przyjmując jako wyjściowy przepływ
. Proces cechowania
rozpoczynamy od nowa przyjmując jako wyjściowy przepływ
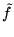 .
.
- (ii)
- Przypuśćmy, że w procesie cechowania nie udało się ocechować
wierzchołka
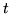 , a żadnego nowego wierzchołka nie da się już ocechować.
Jest oczywistym, że jeżeli przez
, a żadnego nowego wierzchołka nie da się już ocechować.
Jest oczywistym, że jeżeli przez 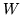 oznaczymy zbiór
wierzchołków ocechowanych to
oznaczymy zbiór
wierzchołków ocechowanych to 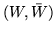 jest przekrojem
rozdzielającym
jest przekrojem
rozdzielającym 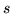 od
od 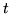 . Co więcej, dla wszystkich
. Co więcej, dla wszystkich
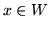 i
i 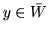 spełniających
spełniających 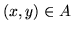 zachodzi
zachodzi 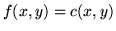 , a jeśli
, a jeśli 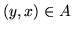 to
to 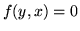 .
Na podstawie uwagi
.
Na podstawie uwagi ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) otrzymamy
otrzymamy
Na mocy uwagi ![[*]](file:/usr/local/lib/latex2html/icons/crossref.gif) oznacza to, że przepływ
oznacza to, że przepływ 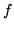 jest
przepływem maksymalnym.
jest
przepływem maksymalnym.





Next: Przepływ całkowity. Zbieżność Algorytmu
Up: Metody sieciowe
Previous: Maksymalny przepływ a dualność
Spis rzeczy
Indeks