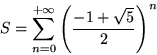Przepływ całkowity.
Zbieżność algorytmu Forda-Fulkersona

Macierzą ograniczeń problemu () jest macierz incydencji grafu zorientowanego. Z twierdzenia i wniosku wynika, że istnieje taki przepływ maksymalny którego wartości na na wszystkich łukach są całkowite. Co więcej, łatwo zauważyć, że całkowite rozwiązanie problemu maksymalnego przepływu można znależć przy pomocy algorytmu Forda-Fulkersona. W rzeczy samej, jeśli tylko przepływ początkowy jest całkowity^8.9 każda iteracja zwiększa wartość przepływu o liczbę całkowitą (liczba $\varepsilon$ o którą zwiększa sie przepływ jest wtedy całkowita). Ponieważ wartość przepływu jest ograniczona przez przepustowość dowolnego przekroju, wszystkich iteracji będzie co najwyżej tyle ile wynosi przepustowość (jakiegokolwiek) przekroju.
W sieci w której przepustowości są liczbami wymiernymi, problem można łatwo sprowadzić do przypadku całkowitego. Wystarczy przemnożyć wszystkie przepustowości przez ich wspólny mianownik $m$. W otrzymanej sieci znajdujemy mnaksymalny przepływ a następnie wynik (t.j. zarówno wartość przepływu $v(f)$ jak i przepływy na wszystkich łukach) dzielimy przez $m$ i otrzymujemy w ten sposób optymalne rozwiązanie problemu wyjściowego.
Ze względu na ważne zastosowania rozwiązań całkowitych problemu maksymalnego przepływu które poznamy w dalszych podrozdziałach, zapiszmy następujący wniosek.

Wniosek 8.6   Jeśli wszystkie ograniczenia przepustowości łuków w problemie () są całkowite, to istnieje rozwiązanie optymalne tego problemu, którego wartości na wszystkich łukach są całkowite. Co więcej, rozwiązanie o tej własności można otrzymać stosując algorytm Forda-Fulkersona.

Niestety powyższe własności algorytmu Forda-Fulkersona nie przenoszą się na przypadek rzeczywisty^8.10. Okazuje się, że można skonstruować prosty przykład sieci o przepustowościach rzeczywistych niewymiernych taki, że algorytm Forda-Fulkersona nie tylko nie dostarcza rozwiązania optymalnego w skończonej liczbie kroków, ale daję nieskończony ciąg przepływów których ciąg wartości nie jest zbieżny do rozwiązania optymalnego! Przykład takiej sieci podajemy za [9].

Przykład 8.3   Zauważmy wpierw, że rozwiązaniem równania rekurencyjnego

$$a_{n+2} = a_n - a_{n+1}, \ a_0=1,\ a_1 = \frac{-1+\sqrt{5}}{2}$$

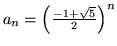
jest $a_n=\left( \frac{-1+\sqrt{5}}{2}\right)^n$. Oznaczmy przez $S$ sumę szeregu $\sum_{n=0}^{+\infty}a_n$,

$$S=\sum_{n=0}^{+\infty}\left( \frac{-1+\sqrt{5}}{2}\right)^n$$

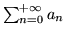
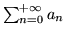
(oczywiście szereg $\sum_{n=0}^{+\infty}a_n$ jest szeregiem geometrycznym zbieżnym).
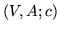
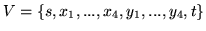
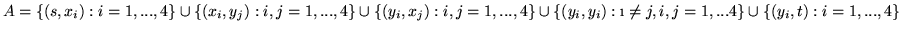
Skonstruujmy sieć $(V,A;c)$ w której $V=\{s,x_1,...,x_4,y_1,...,y_4,t\}$, $A=\{ (s,x_i):i=1,...,4\} \cup \{ (x_i,y_j): i,j=1,...,4\} \cup \{ (y_i,x_j): i,... ......,4\} \cup \{ (y_i,y_i): \i \ne j, i,j=1,...4\} \cup \{ (y_i,t): i=1,...,4\}$. Przepustowości łuków zdefiniowane są zaś następująco. Dla łuków $e_i=(x_i,y_i) ( i=1,...,4)$:

$$c(x_1,y_1)=a_0$$

$$c(x_2,y_2)=a_1$$

$$c(x_3,y_3)=a_2$$

$$c(x_4,y_4)=a_2$$

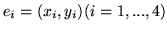
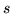
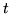
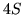
zaś dla pozostałych łuków przepustowości są równe $S$. Jest jasne, że maksymalny przepływ z $s$ do $t$ ma wartość $4S$. Tymczasem algorytm Forda-Fulkersona może postępować następująco:
Początkowym przepływem jest przepływ równy zero na wszystkich łukach.
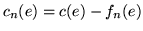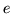
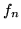
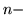
Oznaczmy przez $c_n (e)=c(e)-f_n(e)$ rezydualną przepustowość łuku $e$, gdzie $f_n$ jest funkcją przepływu wyznaczoną po $n-$tej iteracji.
Pierwszą ścieżką zwiększającą niech będzie

$$P_1=(s,x_1,y_1,t)$$

Wtedy

$$c_1(x_1,y_1)=0, \ c_1(x_2,y_2)=a_1,\ c_1(x_3,y_3)=a_2,\ c_1(x_4,y_4)=a_2$$

Następne iteracje definiujemy indukcyjnie. Przypuśćmy, że

$$c_n(e_1')=0,\ c_n(e_2')=a_n,\ c_n(e_3')=a_{n+1},\ c_{n}(e_4')=a_{n+1}$$

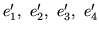
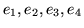
gdzie $e_1',\ e_2',\ e_3',\ e_4'$ są pewnym przenumerowaniem łuków $e_1,e_2,e_3,e_4$. Jako nową ścieżkę powiększającą przyjmiemy

$$s, x_2', y_2',x_3',y_3',t$$

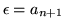
Wtedy $\epsilon =a_{n+1}$ i o tę wartość możemy zwiększyć przepływ wzdłóż ścieżki powiększającej. Otrzymamy

$$c_{n+1}(e_1')=0,\ c_{n+1}(e_2')=a_{n+2},\ c_{n+1}(e_3')=0,\ c_{n+1}(e_4')=a_{n+1}$$

W następnym kroku bierzemy ścieżkę powiększającą

$$s,x_2',y_2',y_1',x_1',y_3',x_3',y_4't$$

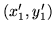
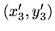
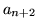
W tej ostatniej ścieżce łuki $(x_1',y_1')$ i $(x_3',y_3')$ są niezgodne (wszystkie pozostałe łuki są zgodne). Zwiększyć przepływ należy teraz o $a_{n+2}$ i otrzymamy

$$c_{n+2}(e_1')=a_{n+2},\ c_{n+2}(e_2')= 0, \ c_{n+2}(e_3')=a_{n+1},\ c_{n+1}(e_4')=a_{n+1}$$

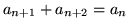
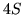
Po takim kroku indukcyjnym w dwóch etapach wartość przepływu zwiększa się o $a_{n+1}+a_{n+2}=a_n$. Nie tylko więc opisane operacje zwiększania przepływu możemy powtarzać w nieskończoność, ale wartość przepływu jest zbieżna do $S$, podczas gdy wartość przepływu maksymalnego jest równa $4S$.